以前、アクチュアリーという職業は、確率・統計という学問を、星の軌道計算や理想的なサイコロを振った場合といった自然科学的な分野から、社会現象的なものに利用を広めたところから始まったという記事を書きました。
社会現象的なものというと、人の身長分布や寿命、人の自殺率といった、一見純粋数学や物理学とは違う身近な?分野です。
同様に1980年代に入って、確率・統計学が金融市場にも応用されるようになりました。私も当初は金融市場には興味がなかったのですが、アクチュアリーの勉強を通して興味が湧き、独学で証券アナリストを受けたりしながら勉強しています。
証券アナリストもCIIAも当たり前のように、株式・債券と言った金融商品の値動きも確率・統計で説明できる前提で話が始まります。
平均や分散の考え方、有効フロンティアンの算出等、勉強を始めた時は”そういうもんなんだ”と、ただ資格試験に受かることが目的で勉強していました。
確かに確率・統計という学問、特に正規分布(ガウス分布)は生物の特徴や測定誤差など、発見された当時は「なんでこんなへんてこな分布(数式)が自然界にこれほどまでに当てはまるのだろう。」と驚かされた、という歴史もあったそうです。
19世紀のベルギーの統計学者ケトレーによって「神は平均人をつくろうとしていた。」(身長が高い人や低い人がいるのは神の誤差=正規分布に従うことが理解できる)という言葉が出来たほどです。ということは自然現象は一般的に正規分布に従うと考えると
株価も正規分布に従う
という考え方は、なんとなく腑に落ちる感じはします。
正規分布(ガウス)分布とは
正規分布は形状からベル(釣鐘)カーブとか、研究結果を残したドイツの有名な数学者ヨハン・カール・フリードリヒ・ガウス(1777年~1855)の名前を冠してガウス分布と呼ばれたりします。
ちなみに正規分布はガウスが発見者ではなく、起源は「ド・モアブル-ラプラスの定理」と呼ばれ、2項分布の計算方法の一つでした。
ド・モアブル-ラプラスの定理
Xが2項分布Bi(n、p)に従っているとき、nが十分大きいならば、Xは平均np、分散np(1-p)の正規分布N(np,np(1-p))に従う。
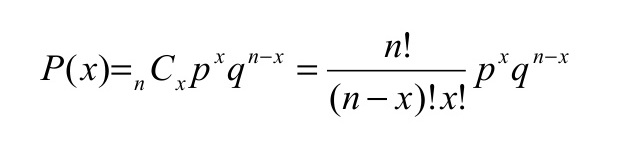
株式のリターンは正規分布か
実際に株式リターンが正規分布となっているか見てみたいと思います。
有名な日本株と米国株のインデックスを比較してみました。分布の考え方は、横軸を月次の収益率、縦軸を収益率の発生頻度(1%刻み)としています。
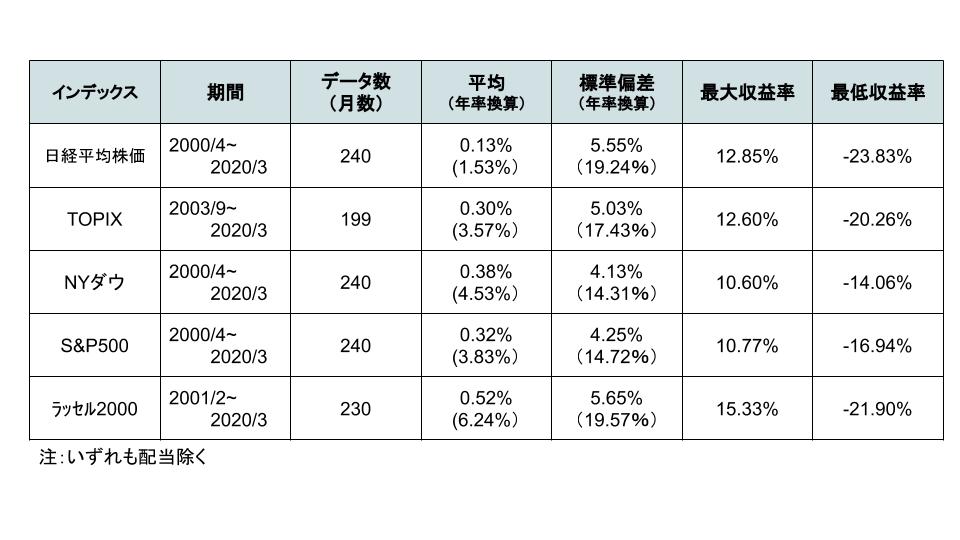
具体例としてTOPIXを挙げると、平均が月次0.30%(※)である(=神様の基本路線は月次0.30%で株価を動かそうとしている)ため、基本的には0.30%を中心とした収益率分布になるはずです。たまに間違えて-10%とかになることもありますが、人間でも身長が2mを超える人とか140cmを下回る人が少ないように、きっとそういう場合は少ないはずです。
※本来ならば、本当の分布(神様が作った分布)の平均(「母平均」といいます。)と所詮240個のデータから算出した平均(「標本平均」といいます。)が本当に一致しているかという検証(検定)が必要ですが、ここでは標本が十分あるから一致していると仮定します。
また、身長とか測定誤差はなんとなく人間がどうしようもない(恣意的でない)自然現象的な事象であるため正規分布に従う感じがしますが、株価は恣意的に上昇または下落させることができるため正規分布に従うか正直疑問です。例えば年収の分布は明らかに正規分布ではありません。
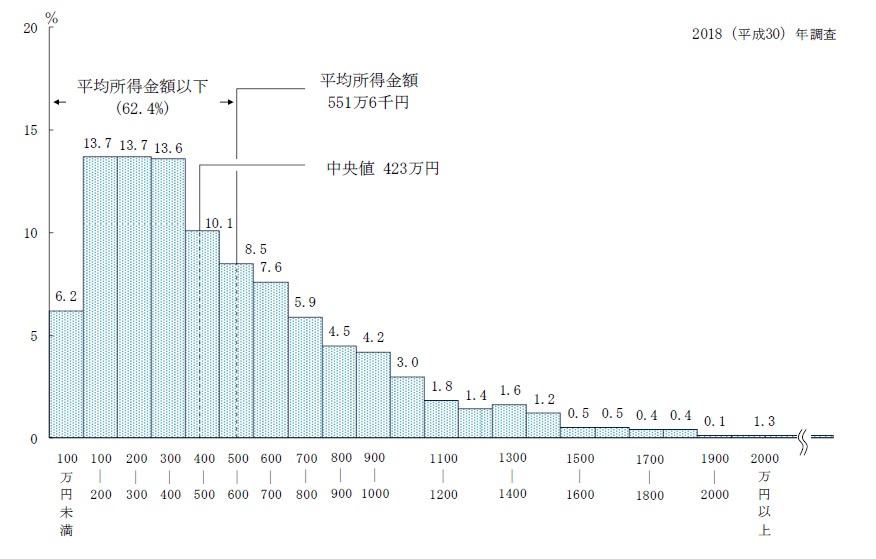
後述しますが、根本的に株価を形成する構造が左右対称じゃありませんし、企業が談合しあったりすれば恣意的に株価を釣り上げることができます。
一方で、対象の会社数を多くしたり、あくまで株価は市場心理により形成される(=人間心理は自然現象)と考えることにより、多少は正規分布で議論できる土台に上げられるのかなと思います。
さて、前置きが長くなりましたが、収益率の実績分布をみていきましょう。
日本株(日経平均株価・TOPIX)
.png)
.png)
米国株(NYダウ・S&P500・ラッセル2000)
.png)
.png)
.png)
本来は「本当に正規分布に従っているのか」を検証しなければいけないんでしょうけど、がっつり難しい話になってしまうので、今回はグラフとして確認するまでに留めました。
というわけで完全に主観ですが、どの分布も一様分布だったりM字分布のような形ではなく、それなりに釣鐘型の分布になっていることが分かりました。また、もう少し平均寄り(尖度が1より大きい)の分布になっているような感じがします。
ブラックスワン(黒い白鳥)の発生状況
あくまで主観的にですが正規分布と比較した場合、実績のほうが平均の周りに末待っていることが分かりました。では、裾のほう(起こりにくいが発生したら影響が大きいエリア)はどうなっているのでしょうか。
正規分布に従っているとすると、平均から離れるほど、生じる確率が小さくなります。
±1σの間の発生確率が約68%、±2σの間の発生確率が約95%となっており、上下2σより離れるような異常値が生じる可能性は5%以下と予想できます。あくまで”正規分布に従っていれば“ですが。
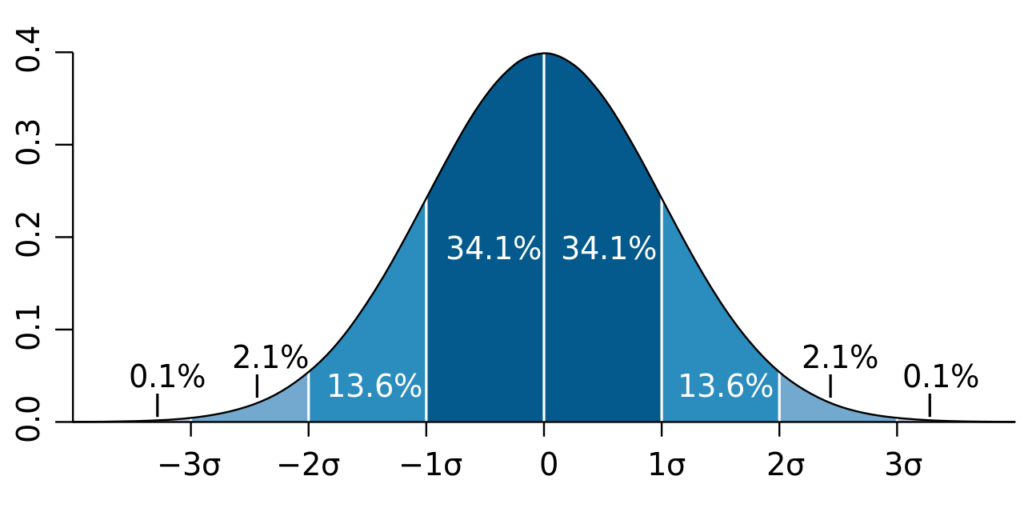
ちなみに、生じる可能性は低いですが、一度生じると大きな影響を与えてしまう事象をブラックスワン(Black Swan)と言います。東日本大震災とかコロナショックとか、当初は発生確率が小さすぎて気にもしなかったことですが、一度生じると社会を常識をひっくり返すほどの影響を与えました。
元ヘッジファンド運用者でもある研究者、ナシーム・ニコラス・タレブが2007年に刊行した著書『ブラックスワン(The Black Swan)』で言及したのがきっかけで、使われるようになりました。従来、すべてのスワン(白鳥)は白色と信じられていましたが、オーストラリアで黒いスワンが発見されたことにより、鳥類学者の常識が大きく覆されたことから、ブラックスワン(The Black Swan)と呼ばれています。
さて、実際にインデックスの実績データに基づき計算しました。
具体的な例で見ると、TOPIXが正規分布に従うと仮定すると、月次の収益率が10.36%~-9.77%の間になることが95%(一般的に言えば”ほとんど”)の確率で起こるということが予想できます。
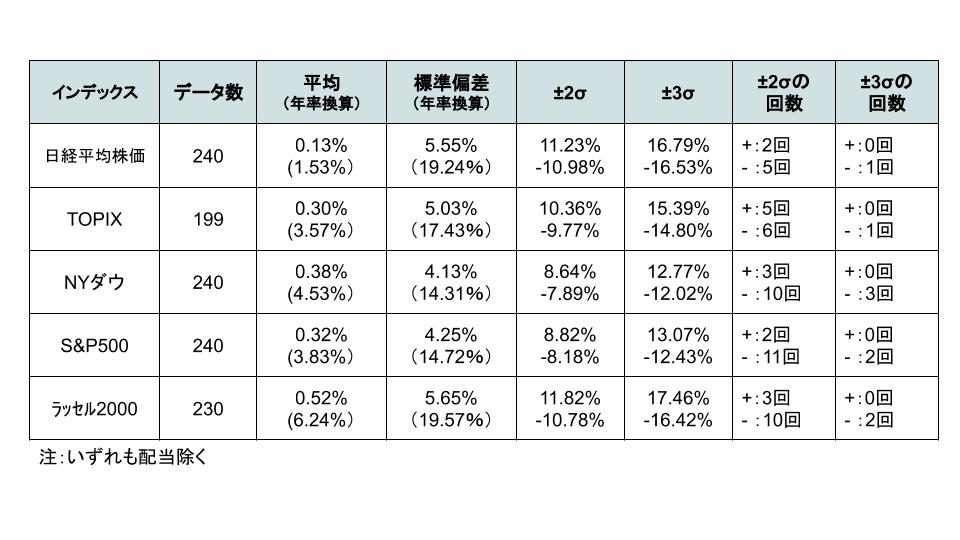
TOPIXのデータ数は199個なので、正規分布だと仮定すると、-2σ(-9.77%)以下になる確率は199個×2.2%(2σより下側になる確率)=4.3個と予想できます。実績は6個ということで、”そんなに離れていないな”という感じです。
一方でS&P500の場合、データ数が240個のため、2σ(-8.18%)以下になる確率は240個×2.2%(2σより下側になる確率)=5.3個と予想できますが、実績は11個ということで、”結構下側の確率が予想(正規分布)より起こりやすいな“という感想です。
いわゆるブラックスワンに近い下側0.1%(1000回に1回起こるか起こらないか程度)という確率の範囲を比較すると、日経平均株価とTOPIXは1回ですので”まぁそんなもんか”という一方で、米国株インデックスはデータ数200程度で2~3回と、1000回に1回という正規分布に基づいた確率に対して少なくとも10倍以上発生確率が高いことが分かります。
注:本当は仮説検定を行って、もう少し定量的に「正規分布に従っているか否か」を判断するのですが、まずは具合を知ってほしいので主観めいた感想で恐縮です。
株式のリターンは正規分布ではない
そもそも株式のリターンの構造を考えると、実は左右対称ではありません。
下の図は、とある1企業の株式のリターン確率をイメージしたものです。株式は有限責任制ですから、投資家(株主)は最大保有株分の損失しか負いません。つまり、投資家の最大損失率は-100%です。
一方で収益のほうに目を向けると、テンバガー(株価が10倍)になる株式の話は聞きますし、Appleは100倍近くになっており、投資家の最大収益率は無限です。
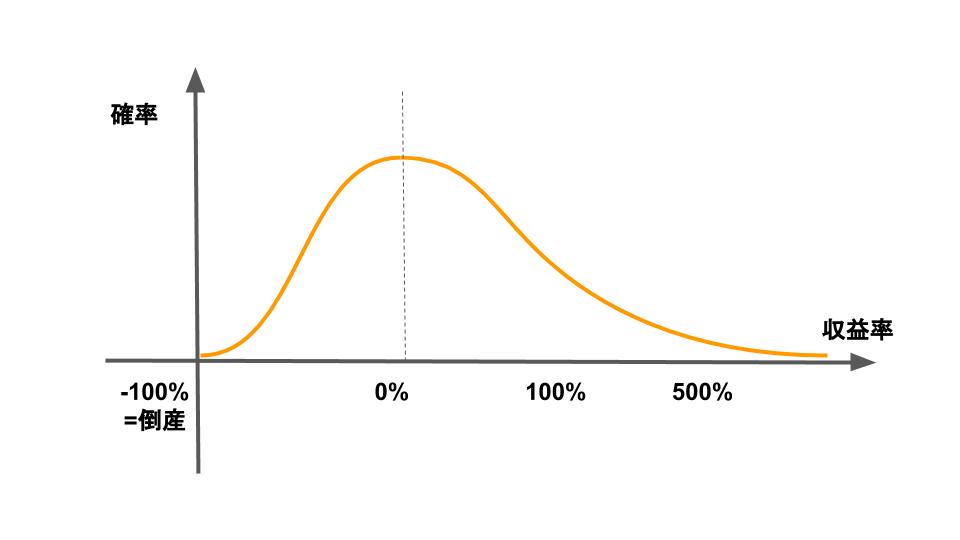
また、経営者も自分の会社をそう簡単に倒産させるメリットもないですし、人間の創造性を信用すれば、自然と株価も上がっていくはずです。1企業で考えれば、時代に合わない企業が淘汰されていくことは否めないですが、マーケット全体で考えれば、栄枯衰退を繰り返しながら成長していくため、基本的には株価はプラスになる動きになると考えています。これはCAPMの前提となる考え方でもあります。
とはいえ、見た感じではそれなりに正規分布に近い形をしています。また、専門ではないので正直良く理解していませんが、中心極限定理に基づくと、どんな分布(一様分布や指数分布様な釣鐘型でも左右対称でもなくても)の合成分布は正規分布に従うとのことなので、インデックスのように何十社・何百社集まった分布は正規分布になるようです。
中心極限定理
「入門確率過程」より
X1、X2・・・Xnが独立で同一分布を持つとき、nが十分大きいならば、もとの確率分布がなにであっても、Sn(=X1+X2+・・・Xn)およびX’(=(X1+X2+・・・Xn)/n)は正規分布に従う。
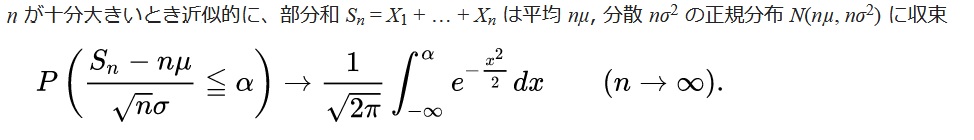
とはいえ、あのGPIFも正規分布を仮定してポートフォリオを構築しているので、実務上は正規分布を仮定して考えても問題なさそうです。






