あまりアクチュアリーらしくない仕事が多かったのですが、というかそもそもそういう仕事だと認識して現職になったのですが、アクチュアリーの知識を披露する場面が出てきました。
それが
データサイエンスの世界
です。
なんとなく統計やモデリングを勉強していたころから、そういう雰囲気はあると思っていたのですが、それは保険料や損害金を計算するガチガチのアクチュアリーがするもので、自分のような、とりあえず社会人として拍を付ける「ゆるふわアクチュアリー」には関係ない話だと思っていました。
このブログでも死ぬほど書いていますが、ARモデル(自己回帰も出る)や赤池情報量(AIC)はもちろん、教科書の最初のほうに書いてあるt検定やらポアソン分布ですらお仕事では使いません。使うのはエクセル関数のみです。
赤池情報量規準(AIC)は、統計モデルの良さを評価するための指標である。元統計数理研究所所長の赤池弘次が1971年に考案し1973年に発表した。
AICは、「モデルの複雑さと、データとの適合度とのバランスを取る」ために使用される。例えば、ある測定データを統計的に説明するモデルを作成することを考える。この場合、パラメータの数や次数を増やせば増やすほど、その測定データとの適合度を高めることができる。しかし、その反面、ノイズなどの偶発的な(測定対象の構造と無関係な)変動にも無理にあわせてしまうため、同種のデータには合わなくなる(過適合問題、Overfitting)。この問題を避けるには、モデル化のパラメータ数を抑える必要があるが、実際にどの数に抑えるかは難しい問題である。AICは、この問題に一つの解を与える。具体的にはAIC最小のモデルを選択すれば、多くの場合、良いモデルが選択できる。
wikipediaより一部抜粋
なので、散々、数学やら損保数理やら生保数理やらお勉強しますが、実務で算式そのものを見ることは滅多にありません。稀に計算システムにエラー値が出たときにのみ「やばいやばい」と言いながら仕様書を見に行く時だけですね。
こんなこと言っていたらアクチュアリー会に怒られそうなので、念のために補足しておくと、やっぱり内側(算式でなく概念)を理解しておいたほうが、つまり、あるパラメータに対して比例的な動きをするのか(1階微分)、加速度的な増え方をするのか(2階微分)、対数的な増え方をするのか(もちろん減り方含む)を予想できたほうが、数字への妥当性の確認=エラーチェックが断然正確になります。
あとは「共通言語」の世界ですね。普通のサラリーマンと会話すると「〇〇が増える・減る」以上のニュアンスがありませんが、やっぱりアクチュアリーと会話すると「どのパラメータに対して、〇〇がどの程度増える・減る(閾値や極地の存在含む)」という表現を含ませてくれます。
野球で言えば(私は野球部ではないのですが)、ボールを投げる動作に対して「投げる」以上の語彙がないところに、「時速〇〇kmで、高さ〇mのところから、回転軸は〇度で、角運動量が〇〇で投げた」という情報がくっ付いてくるイメージでしょうか。これに「だから10%の確率でこの範囲、40%の確率でこの範囲」と予想(示唆)を付加してくれるのは、個々能力のにも寄りますが。
夜遅くの会話となると、冗談半分(別に不要なのに)でホワイトボードに数式書いてみたり、無駄に方程式名を連呼してみたり(テイラー展開とかチェビシェフの不等式とか)と、仕事では関係なのにそれっぽさを出してキャッキャワイワイしていたのが懐かしい思い出です。

あれから数年、方程式の名前を覚えるよりも、仕事では論点がどうのこうのとか、仮説・立証やMECEがどうとか言うことが多くなってきた日々を過ごしていました。
MECE(ミッシー)とは、Mutually Exclusive and Collectively Exhaustiveの略語で、もれなくダブりなくといった日本語に訳されることが多い。各種分析の中で分類やラベリングを行う際に、もれなく全体像(=ユニバース)をとらえきれているか、逆に2つのラベルにダブりがないか、レベル感の異なる軸が混ざってしまっていないかなどを確認する。
しかし、最近になってアクチュアリー用語を耳にすることが多くなってきました。やっと話を冒頭に戻すのですが、昨今DX(デジタルトランスフォーメーション:Digital Transformation)がどこもかしこもで叫ばれるようになり、AIやデータサイエンスという言葉が文系ほぼオンリーのわが職場でも普通に語られるようになってきました。そうすると、分散(ボラティリティ)や正規分布、t分布という言葉も仕事の上で耳になってきました。もちろん、実際に仕事でバシバシ使うというよりも「そういう観点も」という程度の話ですが。
こちとら分散といえば、母分散や標本分散、推定量も一致なのか不偏なのかと、統計の話が出てくれば鼻息を荒くしていますが、実際話すとなると早口で喋ってドン引きされそうなので、大人しく見守っているこの日この頃です。
一方で最近「これって一般常識じゃないんだな。」としみじみ思ったのが、相関関係と因果関係の話です。マーケティングでも良く使われる概念なので、ガチガチに統計を勉強した我々よりも、それなりのスマートなビジネスマンであれば、我々よりも使いこなしていると思っていたのですが、そうでもないようです。
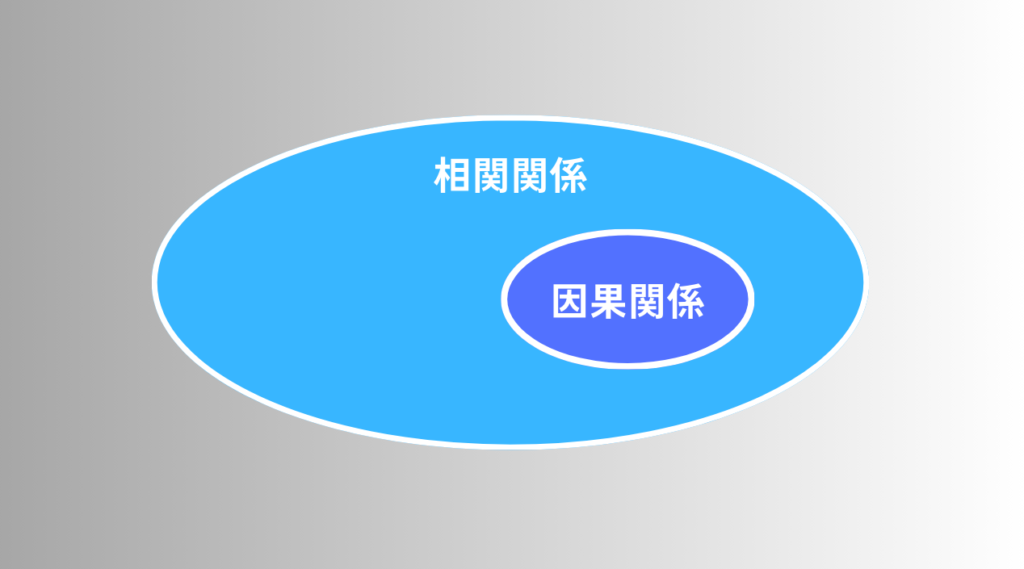
我々(ゆるふわアクチュアリー)は「相関があります」と聞くと、なんとなく数式が頭に浮かんできまして、そこには乾いた計算結果として「相関がある」と認識します。「Aが増えればBが増えた」という結果だけであって、「Aが増えたからBが増えた理由」はまず考えません。傾向があるということを「ふーん」と認識するだけであって、将来の再現性を唱えるわけでもなく、繰り返しになりますが「傾向がある」ことを認識するだけです。
マーケティング等の実務の場合、「将来も同じ傾向が続く」ということが最重要かと思いますが、この時点では
「もしかしたら再現性あるかもね。知らんけど。」
と”まずは”暖かく結果を受け入れます。
とまぁ、このような「相関ある・なし」の会話が最近増えて来まして、その際に良く生じる議論が「これは将来も起こると言えるのか」ということ。気持ちは分かりますが、0.01%でも「生じない確率」があるのならば、ド理系の我々は
「必ず生じる(同じ傾向が確実に続く)とは言えない」
と答えます。99.99%の確率で生じるのですが。
「それは困る」とか「それでは意味がない」という反応が良く返ってくるのですが、こっちは相関という統計量の話をしているのであって、統計に100%の話(「0%」ではない)はありません。(たぶん。)
そして最近気づいたのは、この人たちは因果関係を指して発言しているということです。
「原因とそれによって生じる結果との関係」のことを指す因果関係についての説明はネットにいくらでもあるので、ここでの詳細な説明は省きますが、自分にとって
全然違うやん。
と思っていたことが、世の中では混合されていたことがびっくりしました。ちなみに一回自分はそれで口論寸前までなりました。笑
このようにDXなのかデータサイエンスなのかわかりませんが、知識として確かに有用ではあるのですが、いざ言葉だけが踊り始めてしまうと、それはそれで間違った使い方をしてしまったりとか、正しい使い方をしている人(事)を逆に潰してしまうこともあり得ると思いました。
そういう意味では、データサイエンスはアクチュアリーと非常に親和性が高く、更に言えばアクチュアリーは学術よりむしろビジネスに統計を使っていく人たち、、まさに保険料や損害金の見積りを会社の経営層に説明することを生業にしています。

今後、数学とかもちろん統計等を高校はもちろん大学でも勉強していない人たちがこのようなツールを使い時代がやってくるわけで、それは量子力学も知らない人間がスマホやらLEDライトを使うようなものです。(スマホは電子回路におけるトランジスタで、LEDはダイオードの発光現象を説明するのに量子力学が使われます。)
トランジスタとは、電気の流れをコントロールする部品で、多くの電子回路で利用されています。 電気信号を大きくする増幅機能と、電気を流したり止めたりするスイッチング機能があります。 今日では、スマートフォン、パソコン、テレビなど、身近にある日常的に使っている電化製品のほとんど全てにトランジスタは使われています。
NTTホームページより
我々(ゆるふわアクチュアリー)の次の活躍の場として、こういった”繋ぎ”の役割を担って日常生活に溶け込んでいく世界もあるのかな、と思いました。




