2020年のゴールデンウィークは、ずっと室内での引きこもりを余儀なくされていたため、プログラミング言語のPythonを始めました。
「引きこもりを余儀なく」と言っていますが、コロナ前と比較しても3日に1回は通っているスポーツジムに行けなくなっただけですので、正直大きく生活は変わっていないのが正直なところです。泣
加えて、アラサーが「資産運用→ブログ→プログラミング」と手を付け始めるのが、この界隈の一連の流れな気がして、お恥ずかしい限りです。次は「転職」か「ネットワークビジネス」でしょうかね。笑
さて、Pythonをいじり始めて最初に作ったアウトプットが出来ましたので、記録として残しておきたいと思います。
今回手を付けたのが、「株価収益率」の分析です。
以前もエクセル等を駆使して、株式インデックスの収益率が正規分布に近いのかどうか検証しました。正直やっていることはエクセルでグラフにするのかPythonでグラフにするのかの違いです。
株価収益率の回帰性
回帰性とは「動物がもといた生息場所にもどる性質」のことです。では、株価収益率はどこに「帰るのか」というと”平均“に戻ってくると考えられています。
1990年にノーベル経済学賞を受賞したCAPM理論によれば、最も効率的なポートフォリオは市場の全体の複製です。
この世の中は資本主義社会であり、売り上げがある・革新的な技術を持っている強い企業は成長し、時代に取り残された弱い企業は淘汰されていきます。そのため、強い企業の時価総額は上昇・弱い企業の株価は減少するため、経済の成長=人類の生産性に賭けるののならば、市場全体(=現実的には保有できないので時価総額平均)を持つことは、リターン・リスク効率が最大となるポートフォリオを持つことと同義になります。
結果、CAPMが成り立つのならば、株価の上昇率は「ポートフォリオが対象とする経済圏の成長率」とイコールになり、上下に変動するのは「ノイズ」ということになります。
CAPMでは、個別株式も市場に対する感応度(β)の違いであると説明しているため、個別株式についても同様のことが言えます。

つまり、CAPMが成り立つならば、株価収益率は企業・経済の成長率に回帰し、この自然界におけるランダムなノイズは人間の身長だろうと、ネジの不良品の発生確率だろうと、実験の測定誤差だろうと、正規分布に従うため、「何かしらの成長を平均とした正規分布」に従うと考えることができます。
パッシブ運用はこのCAPMを体現しているのですから、世界の頭のいい人たちはCAPMを信じていると言っても過言ではないでしょう。
株価収益率は正規分布に従うのか
今回は前回同様、日本株としてTOPIX(配当無)、米国株としてS&P500(配当無)を分析対象としました。
各種パラメータの決定
正規分布に従うとしても、正規分布として必要な数値が二つあります。それは平均と標準偏差です。
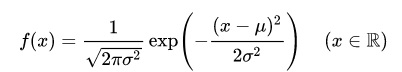
統計学的には過去の事象は将来も続くと考えて、過去の平均と標準偏差を使うことが一般的かと思います。本当は母平均・母分散(本当の平均・分散)と標本平均・分散が等しいことが有意かどうかの検定をしなければならないのですが。
実務的には(特に株式等の金融商品の場合)、過去も続いたことが将来も続くと言い切ることはなかなか難しいので期待収益率(期待リターン)については過去の実績平均の他に、リスクプレミアムから算定するブックビルディング法やブラック・リッターマン法、今後の金利動向や株価上昇にシナリオを作るシナリオ法で使用します。
標準偏差(期待リスク)については、比較的過去と類似するため、実績を使用することが多いですが、各要素(ファクター)に分けて、各要素のリスクを足し合わせて推定する(推定リスク)方法もあります。
なお、世界最大の機関投資家であるGPIFが2020年4月に政策的資産構成を見直しましたが、このときの期待リターン・リスクの見込み方法は、それぞれブックビルディング法・実績リスクを使用しています。
長々と書きましたが、結局過去の実績(月次)を使用しました。いずれも2020年3月を起点として、TOPIXは過去199ヶ月分、S&P500は過去240ヶ月分です。
<TOPIX>
データ数:199
平均:0.31%
標準偏差:5.01%
中央値:0.60%<S&P500>
データ数:240
平均:0.32%
標準偏差:4.24%
中央値:0.93%サンプルコードはこちら。コメントにセンスがなくてすみません・・・
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import scipy.stats as stats
# txt読み込み
iq = np.loadtxt("SP500_date20200520.txt",delimiter=",", dtype = float)
# 計算
n_iq= np.count_nonzero(iq)
mean_iq = np.average(iq)
sem_iq = np.std(iq)
median_iq = np.median(iq)
# 出力
print(n_iq)
print(mean_iq)
print(sem_iq)
print(median_iq)
冒頭の「import」のところでエラーが出る場合は、行列や統計計算に必要なpipがインストールされていないので、インストールしてからデバックしてください。
ここまでの計算結果は、以前エクセルで計算した数値と同じなので、終了です。
実績と分布の比較
パラメータが決まりましたので、実績と分布を比較してみましょう。
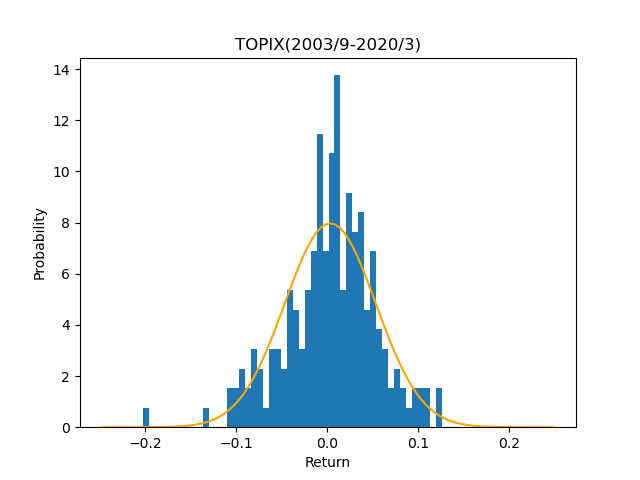
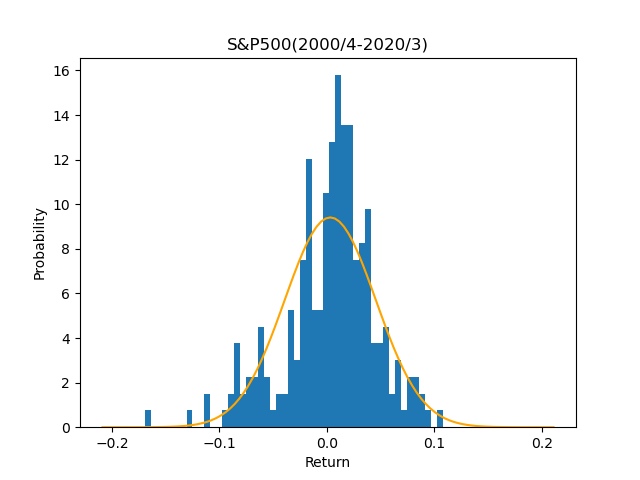
なんとなく釣鐘型(ベルカーブ)になっている気がしますが、実績の方が尖がっています。
もう少し視覚的に正規分布と一致しているか比較する方法が、QQプロットです。QQプロットとは、実績値(測定値)そのものをX軸に、正規分布に従う場合の期待値をY軸にとってグラフにしたものです。 実績値(測定値)を昇順に並べた順位からパーセンタイル(累積確率)を求め、正規分布の確率密度関数の逆関数を用いて期待値を予測します。 プロットが一直線上に並べば、実績値(測定値)は正規分布に従っていると考えらる、というものです。
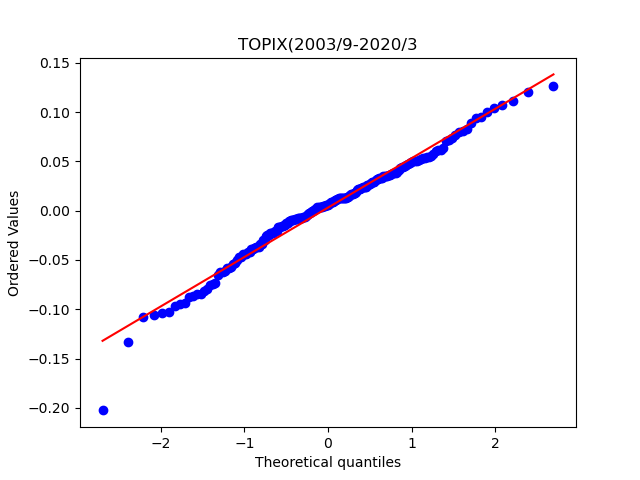
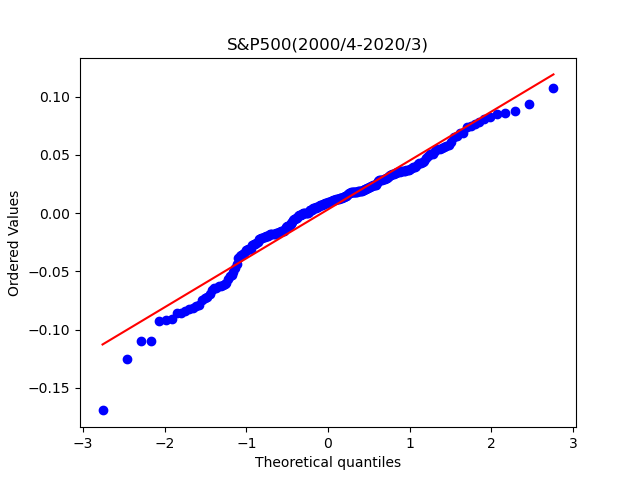
どちらもそこそこ一直線になっているように見えます。TOPIXのほうがより直線になっているような気がします。
サンプルコードはこちらです。パラメータ算定のあとに続いています。
# 正規分布のグラフ作成
mu = mean_iq
sigma = sem_iq
x = np.arange(mu-5*sigma,mu+5*sigma,sigma/10)
y = norm.pdf(x, mu, sigma)
plt.plot(x, y, color='orange', label='Normal')
plt.hist(iq, density=1, bins=50, label='Performance(bins=50)')
plt.xlabel('Return')
plt.ylabel('Probability')
plt.title('S&P500(2000/4-2020/3)')
plt.show()
# QQプロット作成
stats.probplot(iq, dist="norm", plot=plt)
plt.title('S&P500(2000/4-2020/3)')
plt.show()
グラフ作成時の留意点ですが、理論値と実績値を比較するためには、実績値を”正規化“する必要があります。正規化とは「比較・演算などの操作のために望ましい性質を持った一定の形に変形すること。」だそうですが、ここで言う正規化とは”総合計が1”になるようにすることを指します。
理論値の合計は”正規分布の積分”ですので、1になります。一方で、実績値の方は240個のデータなのでグラフの目盛り(スケーリング)が合いません。そのため、実績値のグラフ(ヒストグラム)を正規化する必要があります。
もちろん、一度データ個数の総数で除してから、再度プロットしても良いですが(自分は最初”for”や”if”を駆使して作成しました)、ヒストグラムのコードに”density=1″を加えるだけで正規化できます。
また、一見ややこしいQQプロットも関数「stats.probplot(iq, dist=”norm”, plot=plt)」の一文だけで作成することができますので、少しPythonの便利さを実感した気がします。
正規分布かどうかの検定(シャピロ・ウィルク検定)
ここまで視覚的に「正規分布に従うかどうか」を判断してきました。しかし、アクチュアリーの1次試験やCIIAを受験した身として、もう少し定量的に判断したいと思います。
一般的に、標準偏差が既知である前提で標本平均(サンプルから求めた平均)を検定する方法がt検定、平均が既知である前提で標本分散(サンプルから求めた分散)を検定する方法がχ2乗検定、とあるように「正規分布かどうか」を検定する方法がありました。
サンプル数が十分多い場合はコルモゴロフ・スミルノフ検定(Kolmogorov-Smirnov test)、それ以外はシャピロ・ウィルク検定(Shapiro-Wilk test)を使うそうです。サンプル数の多い・少ないは1000個ほどでしょうか(主観)。
今回はデータ数は200程度なので、シャピロ・ウィルク検定(以下「SW検定」)を使います。また、SW検定は「データは正規分布に従う」という帰無仮説に対して、「正規分布には従わない」という対立仮説を検定するものです。
通常、検定を行う場合、求めていない結果(主張したくない説)を帰無仮説として、求めている結果(主張したい説)を対立仮説とします。結果、反対意見である帰無仮説を棄却に持っていくことで、対立仮説を採択する流れに持っていきます。
最初から「求めている結果(主張したい説)を帰無仮説して、採択すればよいのでは?」と考えるかと思います。しかし、この流れで帰無仮説を採択してしまうと、それは”帰無仮説は棄却されなかった(否定されなかった)“だけであって”帰無仮説が正しいと言える”わけではないのです。あくまでも証拠不十分により棄却できなかったに過ぎません。
ですので、きっぱり否定できた方が結論としては強いので、上記のように、対立仮説に求めている結果(主張したい説)を設定します。
話を戻しますが、こういった論述構成がある中で、SW検定は「データは正規分布に従う」という、今私にとっては欲しい結果(主張したい説)を帰無仮説にしているので、少し留意が必要です。それは最後に説明します。
SW検定の検定量は慣習的にWと書きます。aの式については良く分からないので(Python上は後述のとおり関数で一瞬で出てくるので気にせず・・・)省略します。

結果はこちらです。
<TOPIX>
検定量W:0.9804551005363464
p値:0.007111160084605217<S&P500>
検定量W:0.9650155901908875
p値:1.2951019016327336e-05SW検定の検定値Wとp値を計算する方法は、以下のとおり関数「stats.shapiro(データ値)」を使うだけです。ここでエラーが出る場合は、”scipy.stats”モジュールをコードの冒頭で設定しているか確認してください。
print(stats.shapiro(iq))
検定量Wが1に近ければ近いほど正規分布に従っていると言えるそうです。0.980と0.965といい感じに見えますが、t分布のようにサンプル数が増えると分布の裾の幅が狭くなっていくと同様に、SW検定により採択される範囲も狭まります。(SWの母関数はいくら調べても見つからず・・・)

結果、信頼区間を1%とした場合でも、p値(その事象が発生する確率)が共に1%より小さいため、「正規分布に従う」という帰無仮説は棄却されてしまいました。
つまり、シャピロ・ウィルク検定により
TOPIXとS&P500は正規分布とは言えない。
という結論が出ました。あれ・・・QQプロットはいい感じだったのに。やはりサンプル数が多いからなのでしょうか。SW検定のp値算定の表はn=50が最大だったので、50以上の場合はコルモゴロフ・スミルノフ検定を使った方が良いのでしょうか。
今回はこの辺で。









