参考書(schweser)も一巡して、practice examを解いているこの日この頃です。
最近確率・統計の問題を解いていて、ふとどちらか迷ってしまうのが、分散(Variance)を算出する時に使う分母の数値。分子はもちろん「平均との差の2乗」ですが、分母において毎回「n」か「n-1」で迷います。先に正解を言ってしまうと母分散は「n」、標本分散は「n-1」です。
例えば「日本に住む小学6年生の平均身長」を正確に測定しようと思ったら、日本にいる小学六年生(約11万人)全員の身長を測定しなければいけません。この測定の結果から出てくる分散を、”母集団(N=11万人)の分散”ということで「母分散」と言います。
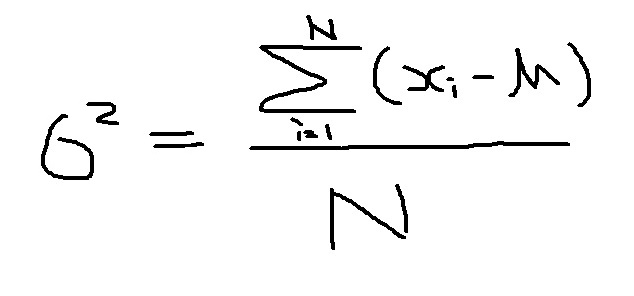
現実的に11万人もいちいち測定していられないので、 現実的な試行回数で母分散を計算(推定)しようと考えたのが、「標本(とあるサンプル群)から母分散を推定する」という意味で「標本分散」という考え方があります。
「標本分散=母分散でいいじゃない」
と思うかも知れませんが、そうは問屋は卸しません。ここで、母分散(本来は統計量全般)の推定の方法の一つとして”不偏推定量”と言うものがあります。
標本から測定した推定量の期待値が母集団のそれに等しいとき、その推定量を不偏推定量と言う。例えば、標本の平均の期待値は母平均に等しいので、標本平均は不偏推定量である。
分散に関して上記の図を算式に表すと
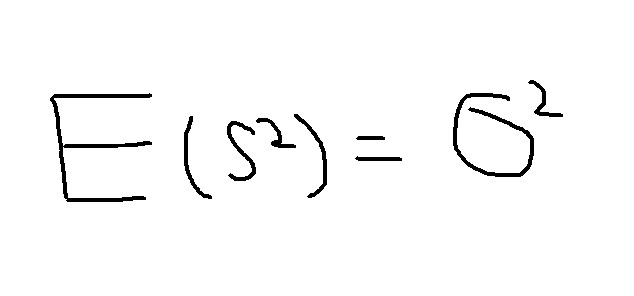
と表されます。実際にこの式を満たす「標本分散(Sの2乗)」を求めてみると
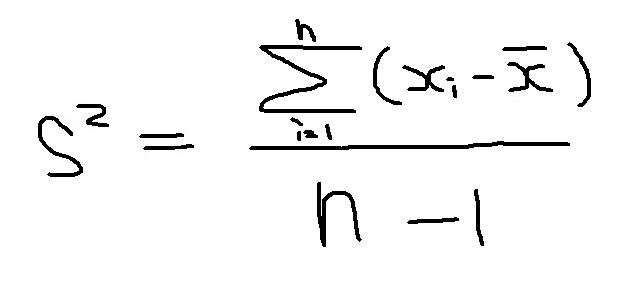
となります。ここで初めて「n-1」が出てきます。ちなみに、標本分散の分母が「n」になるとどうなるかというと
これは単に「標本の分散」でしかありません。
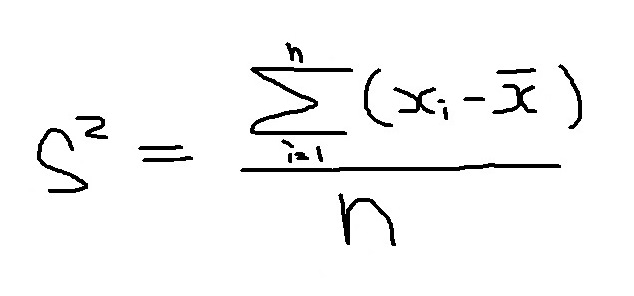
あくまで”n個のサンプル(標本)から母分散を推定する“という作業において、分母がn-1になるというわけです。
小学6年生の話に戻りますが、現実的に11万人もいちいち測定していられないので、母分散は「神のみぞ知る分散」です。というわけで、「母分散を計算しろ」という問題なんて出てくるはずないのですから
とりあえず「n-1」で割っておけばいいや。
と、私はいい加減に覚えてきたわけです。CFAを受験して改めて母集団や標本集団、n-1の意味を理解しました。
ここまで標本分散と母分散で、どういうときに「n(正確にはN)」と「n-1」を使い分けるかわかったかと思いますが、実は私はもう一つの場面で「n」なのか「n-1」なのか迷うときがあります。それは”信頼区間(またはp値)“を計算する時です。例えば以下のような問題を解くときです。
日本人男性5人をランダムに選んで身長を測定したところ、平均値は172cmであった。日本人男性の平均身長の95%信頼区間を求めよ。 ただし、日本人男性の身長の母分散は5.5cm^2であるとし、日本人男性の身長は正規分布に従うものとする。
設問1(分散既知)
日本人男性5人をランダムに選んで身長を測定したところ、平均値は172cmであった。日本人男性の平均身長の95%信頼区間を求めよ。 ただし、この10人の日本人男性の身長の標本分散は5.5cm^2であるとし、日本人男性の身長は正規分布に従うものとする。
設問2(分散未知)
設問1はシンプルな信頼区間の算出です。良く出てくる問題ですが、個人的に母分散が分かっているというのは気持ち悪いです。何せ母分散は神のみぞ知る数値ですから。そういったツッコミは置いておいいて、中心極限定理により母標準偏差(σ)を「nの平方根」で割ったものを使います。
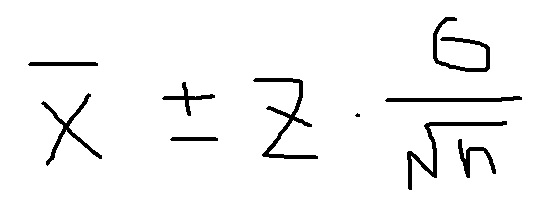
一方で、設問2は分散が分かっていない(未知)ですから、きっと実際に5人の身長を測って、標本標準偏差(s:分母がn-1)を算出したのでしょう。t分布なのも要注意です。そして私が毎回間違えるのは、下図( 母分散未知の信頼区間 )の2項目にある、標本標準偏差を「n-1」で割ってしまうことです。にしてしまうこと。どうしても
分散未知→標本分散→全部「n-1」を使う。
と思ってしまうんですよね。標本分散自体の算出は前述したとおり「n-1」を使うことに加え、t分布の自由度も「n-1」ですし。
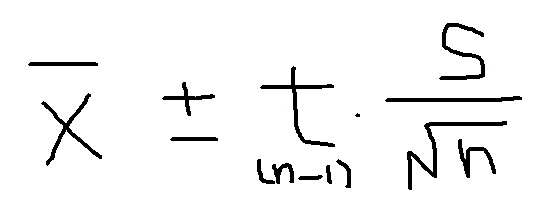
なんでここだけ「n」なのでしょうか。これは中心極限定理から来ている「n」だからです。
中心極限定理
母集団の確率分布が何であっても(一様分布、ポアソン分布等なんでいいが平均はμ、分散σ-2を持つ)、標本平均「(X1+X2+・・・・Xn)/n」の確率分布は、平均μ、分散σ^2/nの正規分布に従う。
中心極限定理に則り母標準偏差σを使いたいのですが、分散未知の場合は、当たり前ですが分散が未知(神のみぞ知る)ですので、致し方なく推定値(=標本標準偏差)を使っているというわけです。そのあとの概念は分散未知だろうと既知だろうと中心極限定理を使うことは同じなので、そこは変わらず「n」を使うというわけです。
このように、それぞれの変数の用途・目的によって「n」を使うのか「n-1」を使うのか、場面分けができたのではないでしょうか。
しかし、ネットで統計学を検索すると、とても充実していますよね。それだけ世の中にたくさん使う人がいるからなのでしょうか。心理学や薬品の効果検証等、世の中的に比較的実務で使うからなんですかね?いろいろ調べものをして不思議に思いました。



