平均では金持ち、可能性ではほとんど貧乏。資産運用でコーシー・シュワルツの不等式を使う。

「天才数学者、株にハマる。」からの面白かった内容のご紹介です。

リンク

よく資産運用のシミュレーションで「平均値」や「中央値」という考え方を使います。「天才数学者、株にハマる。」では、1990年代終わりの”素晴らしい株式市場”に公開市場だけでなくIPO（新規株式公開）も盛んであったが、IPOに投資した人はほとんどのIPO投資家は失敗したと言っています。

時間とお金を合わせて考えてみると、様々な思いをよらない結果を呼ぶことがある。もう一度1990年代終わりの素晴らしい株式市場と、他の人たちはみんな儲けていると羨んでいた時の気持ちを思い返してみよう。（略）

どの雑誌、どの新聞を手にとってもIPOつまり新規株式公開に関する記事や、あなたの1万ドルを1年のほどの間に100万ドルに増やせると豪語する投資の尊師（グル）に関する記事が出ていただろう。しかし、そのころでさえ、その同じ雑誌に、新しい会社が結局日の目を見なかった話や、こんな変動の激しい新規公開市場に投資していては、ほとんどの投資家は投資した1万ドルばかりかシャツに至るまですべてを失うことを主張する、否定的な議論も載っていたのである。

一見矛盾する主張を解明し、統合させるシナリオはこうだ。

参考に、本書が触れている1990年代後半を振り返ると、S&P500指数は1995年の年間34％上昇を皮切りに1999年まで5年連続で20％以上の上昇を記録しました。この間S&P500は459から1469まで上昇しており、5年で約3倍になったことがわかります。

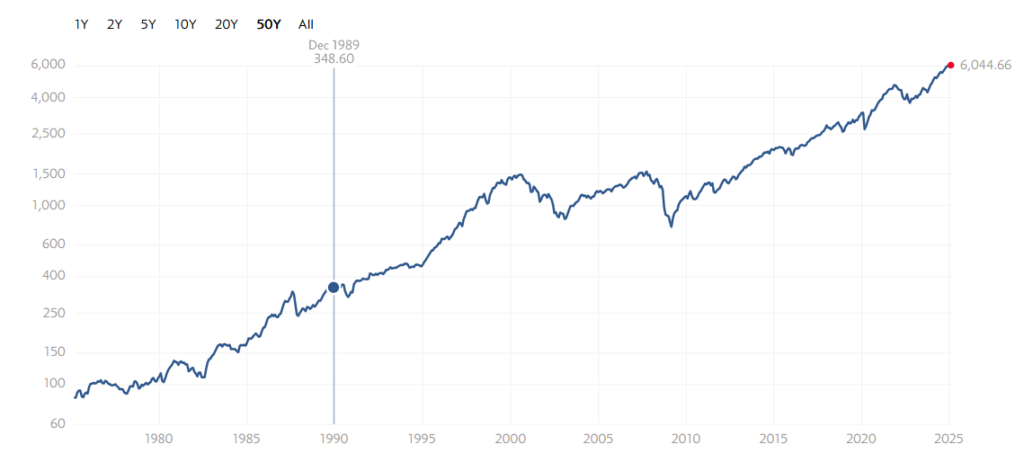
さて、「すべてを失う」とありましたが、公開市場（＝S&P500）が3倍になった一方で、IPO市場は活況ではなかったということでしょうか。本書ではIPO市場ももちろん活況であった一方で、毎年何百ものIPOが行われる中でゴミと化す案件も多く、ハイリスク・ハイリターンであったとのことです。

本書ではこのIPO市場の確率とリターンは以下のように仮定して説明しています。

・50％の確率で80％上昇
・50%の確率で60％下落
※期間は1週間を想定

この仮定における期待リターンは10％で、”平均的には”10%上昇するので十分投資に値するように思えます。

しかし、このパラメータでシミュレーションをしてみると驚くべき結果が得られました。具体的にはモンテカルロシミュレーションを実施し、上記のゲーム（半々の確率で80％上昇か60％下落か）を10回行った結果です。投資なので複利計算しており、例えば2回連続で80％上昇が出た場合、累積で224％上昇（1.8×1.8=3.24）することになります。

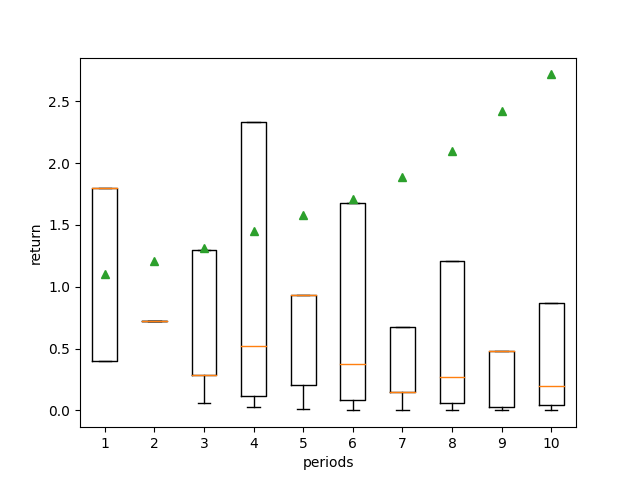
すると平均（▲マーク）はぐんぐん上昇していくのですが

中心値はぐんぐん下落

していきます。

10回目においては、平均値が2.72と概ね平均値（10％上昇）の複利（2.59）と一致しています。一方でちょうど事象数の半分を示す中央値は0.19となっており、このゲームを多数の人数で行った場合、半分の人は80％を失ってしまうことがわかります。

	1	2	3	4	5	6	7	8	9	10
平均	1.10	1.20	1.31	1.45	1.58	1.71	1.89	2.10	2.42	2.72
中央値	1.80	0.72	0.29	0.52	0.93	0.37	0.15	0.27	0.48	0.19

これが「平均では金持ち、可能性ではほとんど貧乏。」の所以です。もう少し詳細に分布をみると、1万のサンプル数のうち、約8000が元本を下回ります。2000程度がリターンを得ている状態（1倍以上）になり、10倍以上になるサンプル数は約500、100倍以上になるサンプル数は約10程度になります。なお、最大倍率は10回連続で80％上昇となった場合であり、この場合360倍になります。

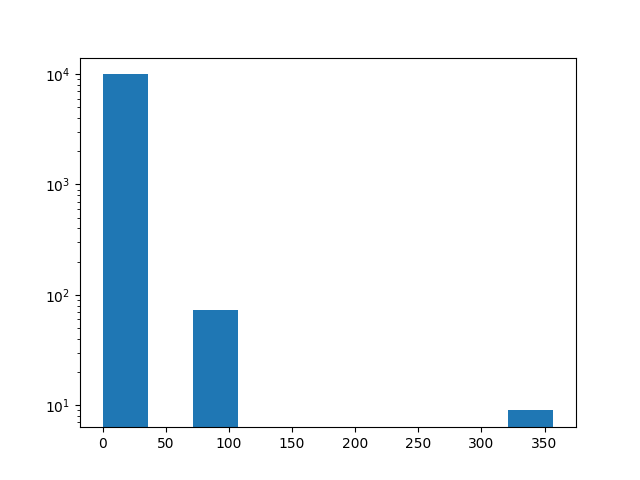
このようにサンプル数が少なくても膨大なリターンを得ているため、平均値を大きく引き上げる効果が生じます。この「中央値＜平均値」という事象は国民の年収分布でもよく見られます。これは数は少ないですが、平均の何十倍、年収何億円という人が1人でもいると全体の平均を引き上げてしまうためです。

所得金額階級別に世帯数の相対度数分布をみると、「100～200 万円未満」が 14.6％、「200～300 万円未満」が 14.5％、「300～400 万円未満」が 12.9％と多くなっている。
中央値（所得を低いものから高いものへと順に並べて２等分する境界値）は 405 万円であり、平均所得金額（524 万 2 千円）以下の割合は 62.2％となっている。

厚生労働省　2023（令和５）年　国民生活基礎調査の概況より

なんとなく平均値ではなく中央値も見るべきということが分かりましたが、このような「平均値の罠」に引っかからないようにするためにはどうしたら良いのでしょうか。それは

算術平均と幾何平均の違い

を理解することだそうです。

算術平均と幾何平均の算出方法の違いはwikipediaに任せるとして、前述の「平均リターンは10％」というのは算術平均です。一方で幾何平均は「√1.8×0.4≒0.85」となるので、リターン換算すると▲15％になります。

確かに「1回づつ1万円」という勝負を繰り返している場合には、算術平均である期待リターン10％でゲームを続けることができます。一方で、資産運用のように1万円を賭けて、1.8万円に増えたとしても再度全額をゲームに賭けなければいけない

複利のゲーム

になったときに幾何平均が効いてきます。

イメージとしては複利の場合、例え2回連続でゲームに勝った（3.24倍）としても次に負けてしまうと、一気に勝ち分が減ってしまう（3.24×0.4＝1.3倍）ことが感覚として分かるかと思います。これが複利の強さであり、怖さでもあります。

なお、算術平均と幾何平均には数学的な関係があり、相加相乗平均やコーシー・シュワルツの不等式とも呼ばれますが、常に算術平均のほうが幾何平均より大きいことが証明されています。

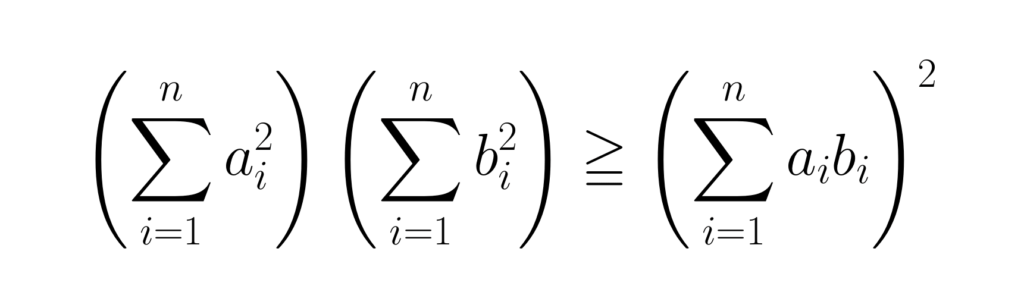
なお、この「算術平均＞幾何平均」をうまく資産運用の実務に応用する手法としてリバランスというものがあります。一般的には「最適なポートフォリオを保つ」「リスク量を一定に保つ」というガバナンス的な要素も強いですが、リバランスを行うことで

常に算術平均取れる

ということが実行できます。

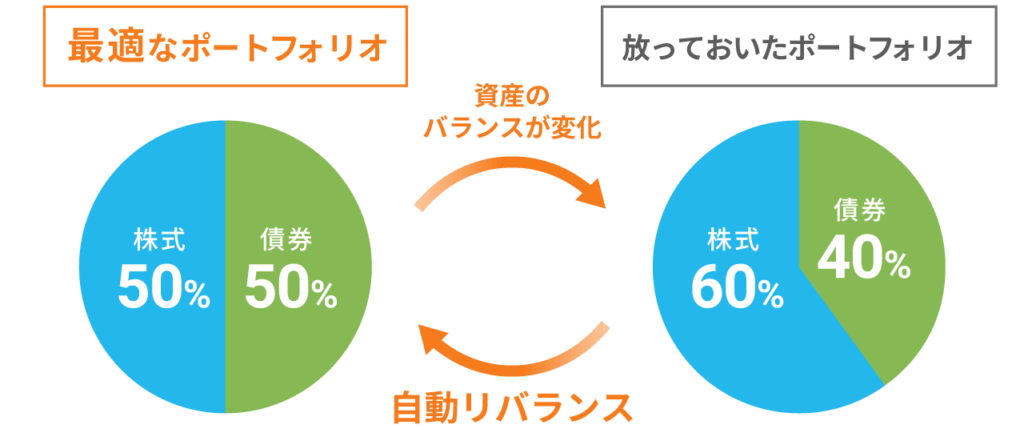
これもイメージですが、例えば株式が好調で、リバランスを”しない”ことで自然と株式の割合が増えてしまいます。そこに株式の暴落が起きれば、せっかく増えた株式リターンが複利効果で最初のポートフォリオの総量より下落幅が大きくなることが分かるかと思います。まさにネガティブな複利効果です。

一方で、適度にリバランスをしていればネガティブな複利効果をヘッジすることができ、下落幅を抑制することができます。もちろんこの数年のように株式が好調な世界では自然に増えた株式がまた増えて・・・というポジティブな複利効果のみを享受できるかと思いますが、いつかやってくる暴落で全てを無に帰す時がやってくるかも知れません。

本書でもリバランスの大切さを以下のように説いていますのでご参考になれば幸いです。