正月にいろいろと定量的な分析をしました。しかし、それは数あるサンプルの中での平均・中央値を語っているだけで、実際我々は一つのサンプルしか取り得ません。
例えば、統計学では「平均値に回帰する」ということが大原則となりますが、そうすると
「10回連続で表が出たコイン11回目で裏が出る確率が50%以上である。」
という結果になってしまいます。実際は「表が何回連続で出ようが次に裏が出る確率は50%」(前提として表裏が出る確率が50%のコインを使っている)ということは変わらないので、状況を可視化すると下図のように経路から大きくずれることはあり得ます。
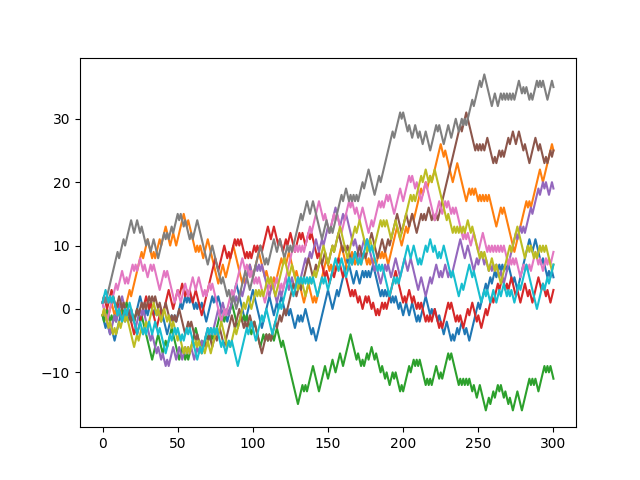
もう少し直感的な表現にすると「割合と差分」の議論になるようです。
表と裏の比率は50%対50%に近づく(大数の法則)。しかし、表と裏の差がゼロに近づいてゆくわけではない。
モンテカルロシミュレーションも含めてコイントスも資産運用も、偶然の結果を観測するという事象には変わらないのですが、一つ大きな違いがあって
資産運用は複利効果
ということです。コイントスの回数のように最初のほうの1回と最後ほうの1回で影響は変わりませんが、資産運用の場合、複利効果で金額も大きくなった次に大暴落が来ると一気に資産額が減少してしまいます。もちろん逆も然りですが。
具体的には下図のように、30回(コイントスのグラフの10分の1に回数にも関わらず)の複利効果で対数グラフ(ログ目盛)で見ないと、一番良かったパターンと一番悪かったパターンが比較できなくなるほど結果が変わって来ます。
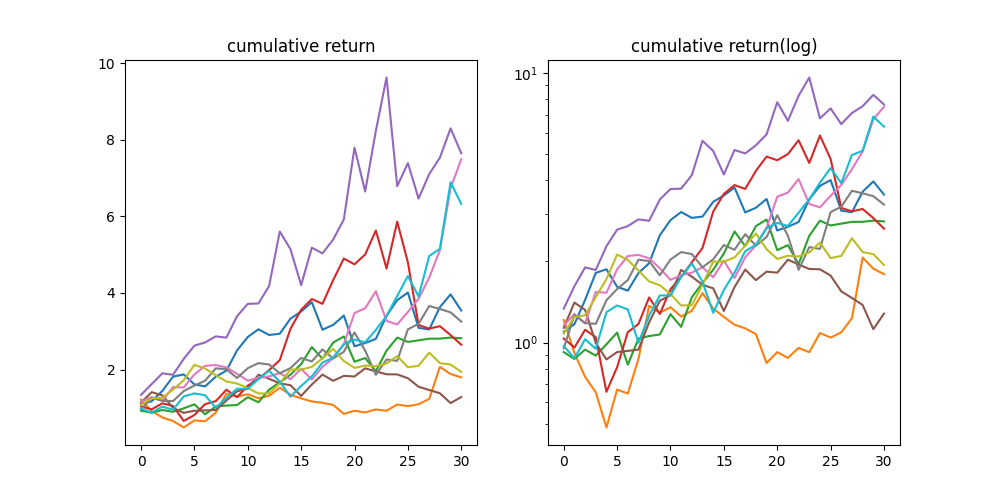
確かに確率論・統計学として平均・中央値で比較する”しか”ないのですが、このような認識との違いはきとんと認識しておかなければなりません。
ちなみにこの確率論における認識との相違には既に言葉があって
ギャンブラーの誤謬
と呼ばれています。
ギャンブラーの誤謬(ギャンブラーのごびゅう、英語: gambler’s fallacy)とは、ある事象の発生頻度が特定の期間中に高かった場合に、その後の試行におけるその事象の発生確率が低くなる(あるいは逆に、ある事象の発生頻度が低かった場合に、その事象の発生確率が高くなる)と信じてしまうという誤謬である。
wikipediaより
なお、「誤謬(ごびゅう)」とは「思考内容と対象との一致しない思惟、判断」とのことで真理の反対語だそうです。
コイントスの話に戻ると、5回連続で表が出る確率は1/32なので、4回連続で表が出た後に「次のコイントスでは裏が出る確率」が高くなっていると思う人がいるかもしれませんが、これは誤りであり、まさにギャンブラーの誤謬の一例だそうです。「5回連続で表が出る」という事象と、「4回連続で表が出た後、5回目に裏が出る」という事象では、どちらの確率も等しく1/32です。
一方で、誤謬とは言い切れない場合もあります。コイントスで連続して裏が出た場合、ギャンブラーは裏が出る確率が高くなったと判断することもあるということです。これは、コインが公正ではない可能性を念頭に置いた合理的な結論であり、これは誤謬ではないとされています。
「天才数学者、株にはまる(ジョン・アレン・パウロス)」によれば、「コイン投げの結果は裏表半々を中心とした確率論的ゴムバンドに支配されていると信じている」ことがギャンブラーの誤謬だと言っています。
コイン投げの裏表に連続して賭けている2人について、コインが公正であるのならば二人のうち1人がリードする可能性と他方がリードする可能性は同じだが、2人のうち1人が、このどちらかと言えばつならない競争のほとんどの間、リードを保つ可能性が高い。
数量的に述べれば1000回のコイン投げをすれば、片方が全体の時間の96%以上でリードを保つ可能性が、2人のいずれかが全体の時間の48%から52%でリードしている可能性より高い。

なお、今回の仮定において資産運用(主に株式投資)もコイントスのように「毎回事象がランダム(過去の事象と発生確率が独立している)」という前提を置いています。
一方で、このモデルを否定するモデルも世の中には多く存在していることに留意が必要です。
https://www.imes.boj.or.jp/research/papers/japanese/kk23-b2-2.pdf
本稿では、証券市場で観測されるアノマリーの1つである、証券価格の変動にお
ける短期的に生じる正の自己相関(モメンタム現象)と長期的な負の自己相関(リバーサル現象)に焦点に当てて、分析を行った。具体的には、①日本と米国の債券と株式の日次、週次の先物価格データでこれらの現象が観測されるか否かを調べた。
その結果、米国ではモメンタム現象とリバーサル現象の両者が、日本ではリバーサル現象のみが、それぞれ観測された。これは、行動ファイナンスの解釈に従えば、これらの市場では、投資家の過小反応と過剰反応が発生していることを示唆している。また、株価データを用いた多くの既存研究では、モメンタム現象は、欧米市場では観察されるが日本市場では観察されないということが指摘されているが、本稿の分析結果は、それと整合的である。




