2024年も気づけば5月中盤。かなりざっくりではありますが、今年も半分が終わろうとしています。個人の運用実績は株高・円安のおかげで今のところ順調に推移しています。
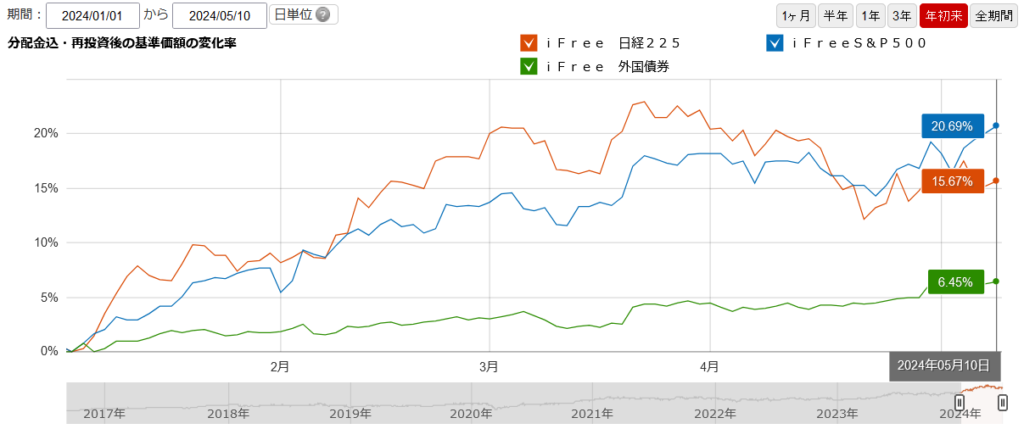
問題があるとすれば、これだけ円安相場になってしまったことによる円高への逆流懸念や、個人的にはあまり期待していない国内株式も珍しく順調に推移しているので「何に追加資金を投資すればよいのやら」と悩んでいます。ただし、今のところまとまった資金もないので、ただただ市場をウォッチしている毎日です。
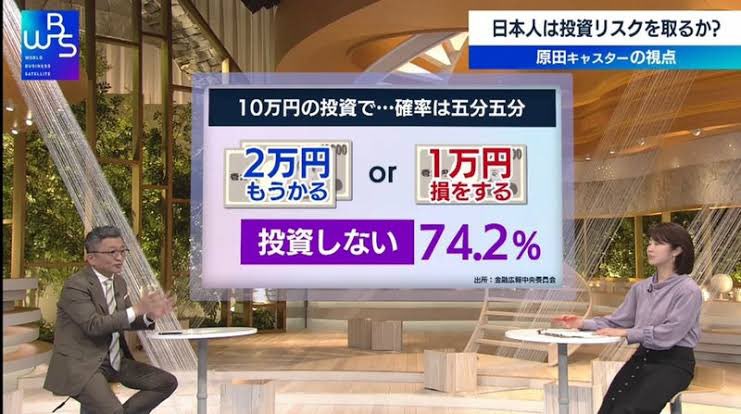
年初から順調だった株式マーケットですが、4月に入ってから調整も入り、新NISA勢にとっては初めての試練を迎えているようです。とはいえ日経平均も41000円から39000円程度に5%下がっただけですが。とはいえ、テレビ等でも新NISA勢向けなのか、「投資のリスク」に関する内容の報道が多くなったように思います。
その中で「日本人は成功する確率が五分五分でも大半投資しない」という内容のものがありました。日本人はリスク許容度が他国と比較して低い(成功することよりも失敗することを嫌がる)ということを紹介しています。確かに投資は「ギャンブルか?」と聞かれると、日本の世の中の認識である「確率的に損を被る事象」をギャンブルと定義するのならば、「ギャンブルでないとは言えない」と回答せざる得ません。最近「わが投資術」という著書で有名になった清原達郎氏も
儲かりやすいギャンブルです。
と取材等で明確に回答しています。
投資もギャンブルであれば、パチンコや競馬は悪くて、投資は良いのでしょうか。そうすると、資産運用のプラットフォーム(SBI証券や楽天証券等)が同様に勧めてくるFXや仮想通貨はどうなのでしょうか。
その答えは「期待値」だと考えています。例えば今回「日本人はリスク許容度が低い」と例に出すために使われた事象は、10万円投資して「12万円になる確率は50%」「9万円になる確率が50%」という前提です。確かに、古い感覚で見ると「半分の確率で1万円損してしまう」ということからギャンブル性は否めません。
これをどのように良いギャンブルなのか悪いギャンブルなのかを見極めるかというと、期待値を計算する必要があります。実際期待値を計算してみると、「12万円×50%+9万円×50%」で10.5万円となります。
期待値は、確率的に得られる値の平均値のことです。 起こりうる事象で得られる値とそれが起こる確率の積を足し合わせて求めます。 確率分布を扱うなかで使われる場合には単に「平均」と呼ばれます。
10万円の参加料払って、”平均的には”10.5万円を手にすることができるため。5000円の儲けを得ることができます。実際、前述の期待値論に関しては同じ考えを持っています。
儲かりやすいギャンブルです。宝くじの期待値40%は~50%。つまり100円使えば平均40~50円戻ってきます。競馬、競輪、競艇は75%。それに対し株式投資は100%以上の期待値になると私は思います
週刊エコノミストOnlineより
ただし、これでも投資に関してのギャンブル感を拭えないかと思います。期待値がプラスだからって、その賭け事に参加するのはその時1回です。「平均的な期待値がプラス」だからと言って、損するか得するかには運要素があるため、どうしても損をしたときの想像をしてしまいます。
そこでその不安を払しょくする考えが
大数の法則
です。
確率論・統計学における基本定理の一つ。確率の公理により構成される確率空間の体系は、統計学的確率と矛盾しないことを保証する定理である。
たとえばサイコロを振り、出た目を記録することを考える。この試行回数を限りなく増やせば、出た目の標本平均が目の期待値である3.5の近傍から外れる確率はいくらでも小さくなる。これは大数の法則から導かれる帰結の典型例である。
wikipediaより
期待値は確かに1回しかできない事象では空想の数字になりますが、その事象をたくさん行うと、原則論として結果が期待値に収束していきます。前述の10万円を投資する例では、確かに1回だけだと「1万円損する」確率は相応にありますが、100人が同時に行う、または100回事象を行うのであれば、それこそ大数の法則で勝つ確率が抜群に上がります。
具体的に「損をする」確率を考えてみたいと思います。試行回数(チャレンジ回数)が10回であれば「6回以上負ける」と損になので、6回以上負ける確率(6~10回負ける確率の合計)を計算すると、その確率は17%まで下がります。このように試行回数を増やしていって負ける確率を計算すると、30回の場合(11回以上負ける)約2%、100回の場合(67回以上負ける)約0.04%と、どんどん負ける可能性は低くなります。
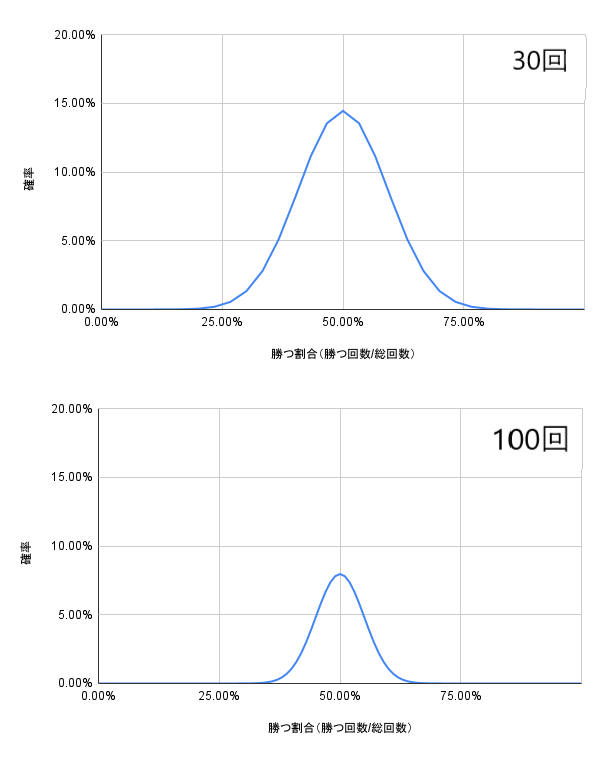
回数による勝率の確率分布を見てみると、10回であろうと30回であろうと100回であろうと、損益分岐点は勝率33%になります。(3回に1回勝っておけばマイナス収支になることはない。)しかし、回数を重ねるほど、裾の太さが狭くなっていることが見て取れます。具体的には横軸(=勝率)25%を比較すると、30回のグラフは少し隙間があるのに対して、100回のグラフはほぼ横軸と重なっています。
これは回数が増えるについて、確率が期待値周辺(=5千円勝つ事象)に寄っていくため、当たり前と言えば当たり前の結果となります。なお、逆に言えば期待値が負の場合は、どんどん試行回数が増えるに連れて負ける可能性が高くなることを物語っています。
このようにギャンブルであろうと投資であろうと確率・統計の話に結局はなるので
成功=期待値×試行回数
という方程式が存在し、いかに「期待値を上げるか」「いかに試行回数を増やすか」が勝つ投資への近道になります。それならば、実際にこのようなゲームがどこに存在しているかとというと、まさに株式や債券投資になります。
基本的に株式や債券は、キャピタルゲインや配当・クーポン等のインカムゲインを通じて、投資家全員にリターンを配るゲーム、いわゆるプラスサム・ゲームであるため、期待値はプラスのゲームです。それなら試行回数はどうやって増やすのかというと、それは「いかに市場に残るか」という目線になります。
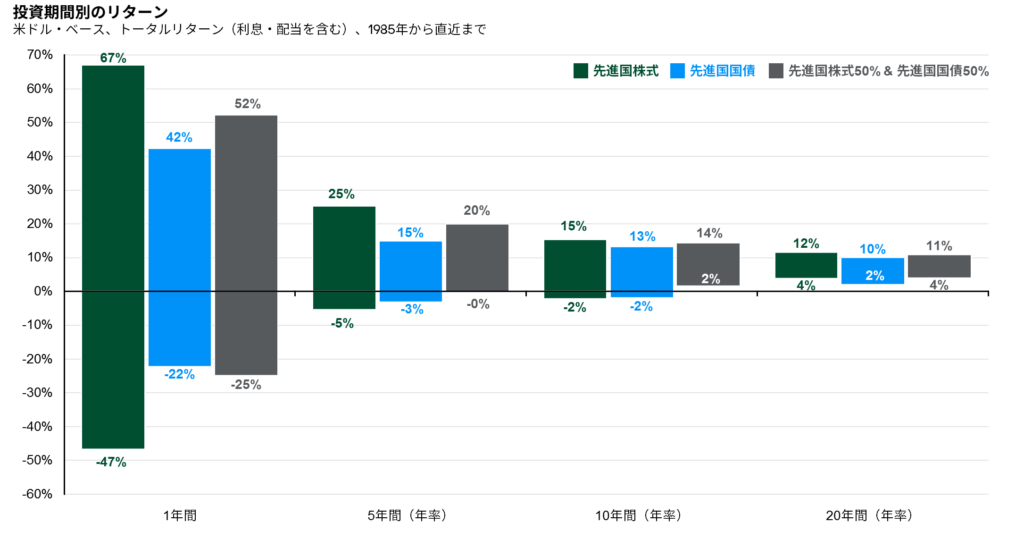
時間分散効果とも呼ぶことがありますが、過去の歴史を確認すると、長期投資になればなるほど
負ける確率は少なくなります。
ここまでくるとなんとなく想像がつくかと思いますが、競馬やパチンコは胴元がそれなりのコストを回収するので期待値がマイナスであることは明確ですが、FX(為替)うあ仮想通貨は所詮通貨の交換でしかなく、いわゆる「ゼロサム・ゲーム」(=期待値がゼロ)に該当するので、株・債券とは性質が異なることが分かります。
また、レバレッジを掛けるということも、この考え方から不適切な手法であると言えます。レバレッジも信用取引であるため、負けすぎると強制清算(=強制的な退場)が待っており、言い換えれば試行回数を十分にこなす前にゲームが終了してしまいます。大数の法則はある意味、勝ち続けているといつか負ける・負け続けているといつか勝って期待値に収束するという逆張り戦略であるため、いかに長期間試行回数をこなせるかが「(勝つことではなく)負けないゲーム」にする重要な要素となってきます。

専門的話になりますが、前述の期待値や試行回数に加えて「ブレ(標準偏差)」というのも重要な要素になってきます。具体的には「50%の確率で4万円貰える・50%の確率で3万円失う」という、期待値が5千円と先ほどのゲームと同じです。しかし、同様に30回、100回と収支がマイナスになってしまう確率を計算すると30回は約10%(前述は2%)、100回は6.7%(前述は0.04%)と確率が上昇しました。
これはブレが大きくなったことで、損益分岐点が勝率42%に上昇してしまったことが要因です。一方で、勝ち続けたときの賞金は大きくなっているので
「ゲームが不利になった」というわけでなく
「負けない確率」で考えると悪化したということに留意が必要です。
これを株式投資に当てはめてみると、個別株・小型株に投資することだと思います。個別株・小型株になるほど会社が潰れる(株式価値がゼロになる)可能性が存在し、その一方で10倍・20倍のリターンを狙うことができます。一方で、大型株、さらにインデックス運用になると、ある程度成熟しているので潰れることがない(インデックス運用に関しては市場価値がゼロになることは考えづらい)一方で、上値も限られます。
少しアカデミックに考えることにより、自分がなんとなく投資方針で決めている
・個別銘柄はやらない
・FXはやらない
・レバレッジはかけない(ショートも)
について言語化できたような気がしました。もちろん10倍になるという夢は見ることはできないのですが、。
リンゴが木から落ちるように、この世の中で生命保険がちゃんと機能しているように、この世界に元来から存在する機能を活用して、投資に才能がなくても運要素を極力まで排除して、誰でも再現性を持って勝てる戦略を愚直に続けていこうと思います。




