台風で12試合中4試合が中止となり、1等倍率が256倍になっていた第1476回のMEGABIGの結果がでました。
土曜の夜に締め切りとなって、全試合が終わる日曜の夜には結果が出るそうなのですが、今回は話題性があったせいかなのか、通常の回に比べて売り上げが10倍だったせいか、結果発表も延期となるトラブルがありました。

公式からおも月曜9時とのアナウンスがありましたが、結局11時~12時ごろに公表になっていました。
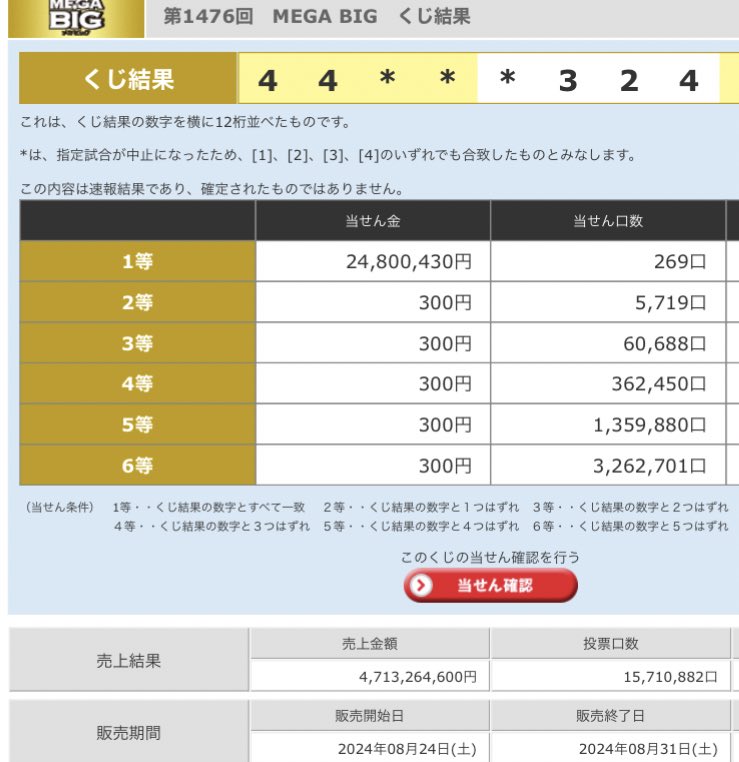
さて、結果はというと、1等がやはり269口も出たことがあって、当選金は2500万円ほどとなっていました。前回の記事でも書きましたが、通常1年間(全60回ほど)で数口しか出ないのですが、今回は1回でこれです。確率が256倍になっていたということで、通常の12回開催であれば今回も1等は1口だったのではないでしょうか。
加えて1等が多く出たこともあり、分配する数も増え、当選金額も通常数億円であるのにもかかわらず、
1等であっても2500万円(全然メガじゃない。笑)
でしたし、2等以下はまさかの300円統一です。なお、キャリーオーバーが58億円あったから1等もこの金額を保てましたが、後述しますがキャリーオーバーがなければ1等の金額は300万円程度だったと予想できます。これは今回参加者が多かったわけでもなく(参加者が多ければ分配する人数と当選金総量の両方が比例するため関係ない)、やはり単に確率が256倍になっていたことが理由です。
ちなみに2等以下の当選金が下限の300円に張り付いたことにより(計算上は数十円)、本来35%が1等に分配されるはずだったものが2等に吸い取られ、1等のキャリーオーバーを除く当選金総量(=純粋なそのゲーム内だけのファンド量)が16億円から8億円へと半分程度になっていました。これにより理論上1等の当選金額は32百万円だったものが低下しました。6等は300円ではあるのですが、人数が300万口以上と想定されるため、当選金総量は1等の8億円より多く、10億円近くになっています。
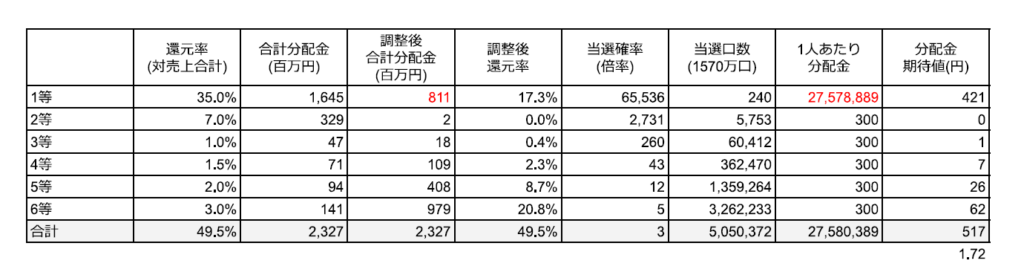
加えて理論上1等の当選口数は240口程度(1570万口÷6.5万)だったものが29口上振れて269口となっていました。これにより当選金はさらに低下し、これを考慮するとだいぶ公式の当選金の金額が再現できました。(自己満足)
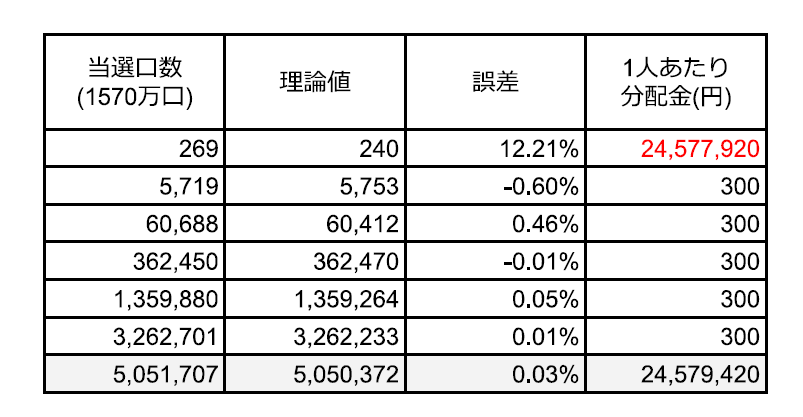
やはり1等は口数が少ないので理論値から12%もぶれましたが、2等以下は数が多くなるについて理論値とのずれがなくなっていきますね。まさに
大数の法則が成り立っている
ことが分かりまして、6等になるとその後差は0.01%にまで低下します。
さて、7000万円以上購入した方の結果も出たようです。なんと結果は1等8本!当選金額2億2千万円!ということで見事3倍に増やしていました。純粋に羨ましい。しかも非課税。
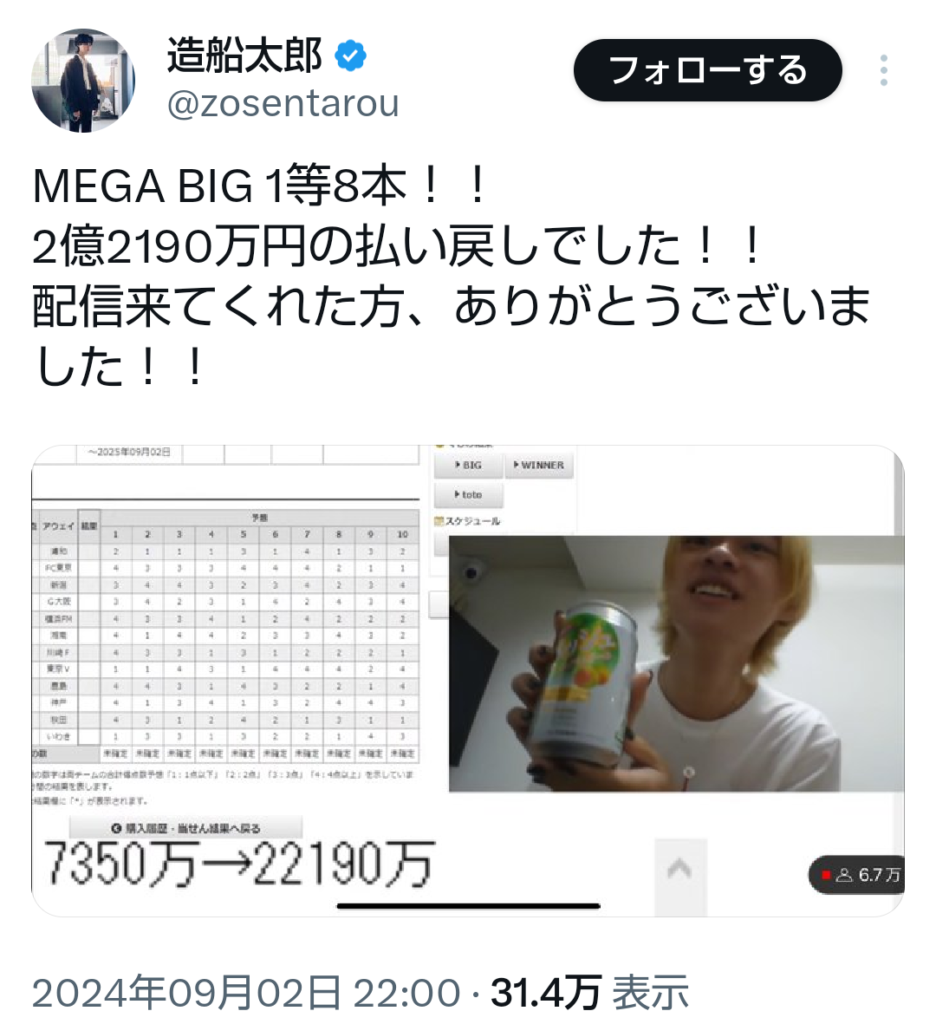
もちろん7000万円つぎ込んだ精神力・行動力も凄いことですが、統計的に計算してみると
運用要素も大勝利だった
ことがわかります。購入額が7300万円ということで、口数は約24.5万口だったことがわかります。1等の確率は「6.5万分の1」ですから理論上の1等数は3.7本でした。また、2位以下の当選金額が300円統一だったことを考えると、今回のゲームは「1等を何本当てるか」に尽きるかと思います。
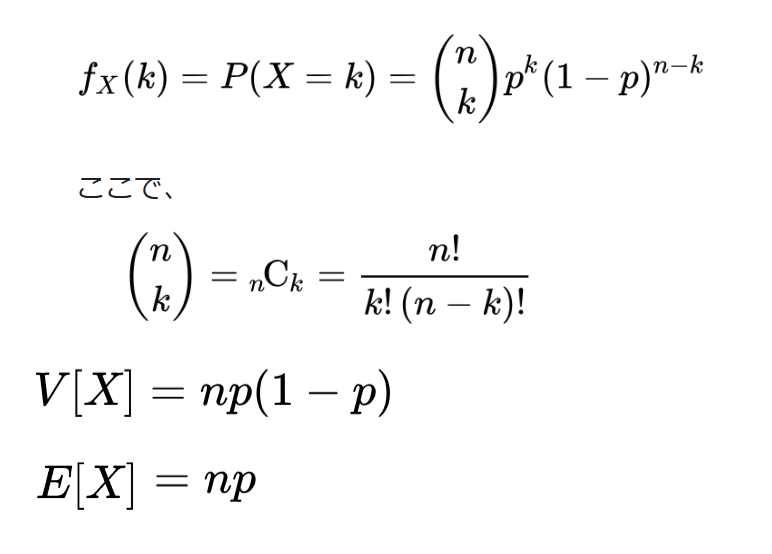
一応、2等以下の当選金も考慮したいと思います。理論上「2等以下が当たる確率」は32.1%となるので、245,000口買った場合、300円の塵が積もって約2350万円になります。実際の2等以下の当選金は2350万円(22,190万円-8本×2,480万円)ということで完全に一致しており、大数の法則に感激です。
そうすると、以下の通り、確率論上のこのゲームの全体像が見えてきます。ネットでは「25万口買えば十分大数の法則が成り立つのではないか」という意見も散見されましたが、1口づつ買うゲームに対して約25万口を一度買ったことによる大数の法則は確かに効いてきます(2等以下はまさにそれ)。しかしそれはn=1のベルヌーイ分布に対しての大数の法則にしかすぎません。1等を当てる確率は小さいので、更に
「25万口を1度に賭ける」ゲーム
というn=25万の2項分布が生成され、この2項分布を繰り返す(25万口一度に買うゲームを何度もする)という大数の法則がまた別に存在します。ここについて考えたいと思います。
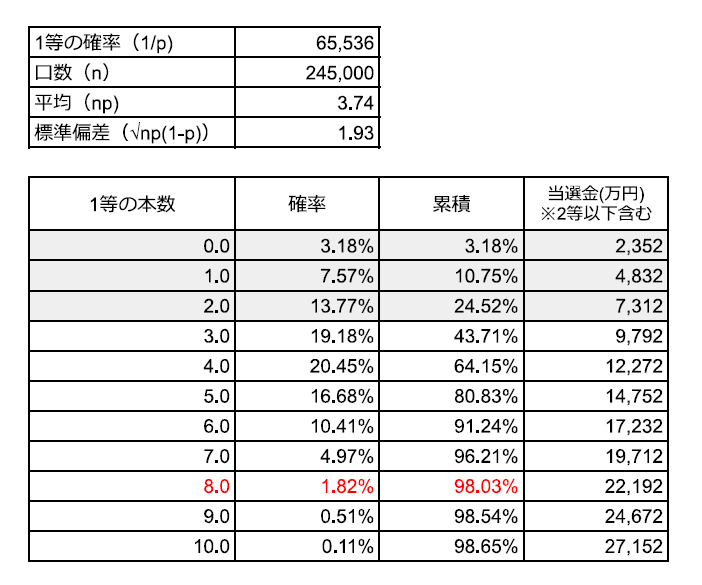
前置きが長くなりましたが、実は「1等を8個以上当てる確率」というのは非常に低く(約3%)、「1等が1つも当たらない確率」というワーストシナリオと同じくらいであることがわかります。さすがの強運としか言いようがありません。
「負けない」どころか「圧倒的勝利」です。
本人も取材に対して、運要素がかなり利いたことを認識されていました。25万口買った場合の1等の平均は3.7本でしたが、元本を毀損する確率が25%ありました。
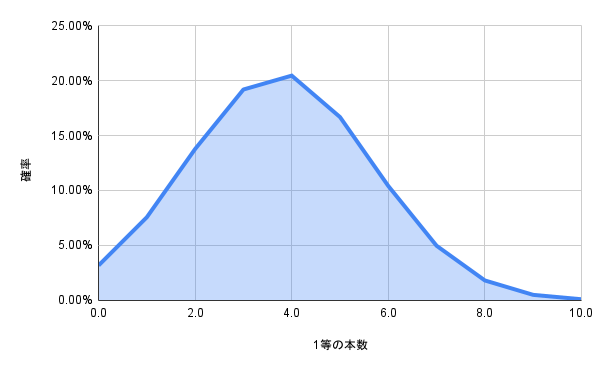
勝率が75%ということなので、確かに有利なゲームですが、1等が1本も当たらない=約5000万円損する(2等以下の当選金は入るが)という確率も3%存在していたので、一般人にはこの3%は非常に重くのしかかります。このゲームを何回もできると仮定すると、80%の人は5本以下に収まってしまうのに対して、この人は1回の参加で上位2%を引いたわけですから凄いです。
お金が減らなかった、負けなかったと安堵しましたが、そのときはスプレッドシートで確認作業をしていたので自分も信用しきれなくて、ちょっと本当かなという部分はありました。でも確認したら当たっていた。今回は1等が1本も当たらないぐらいの確率を上振れで引いたんで、相当良かったです。
さて、次は「次回台風が来たら自分は参加するのか」を考えたいと思います。
振り返ればこのゲームには「台風が来て試合がちょうど4試合中止となった(5試合になると”くじ”そのものが中止)」という以外に、以下の2つの外的要素がうまく作用していました。
- キャリーオーバーがあった
- 売り上げが100億円を超えなかった
前述しましたが、当選する確率が上がることはうれしいですが、その分分配する人数も増えて1等の当選金が小さくなります。実際、1477回はキャリーオーバーがなくなっていました。実はキャリーオーバーがなかった場合、1等の当選金は3百万と算出できました。そうすると今回の1等である2500万円のうち、残りの2200万円がキャリーオーバーから生じていることになります。58億円を260人で割ると、まさに2200万円に一致します。
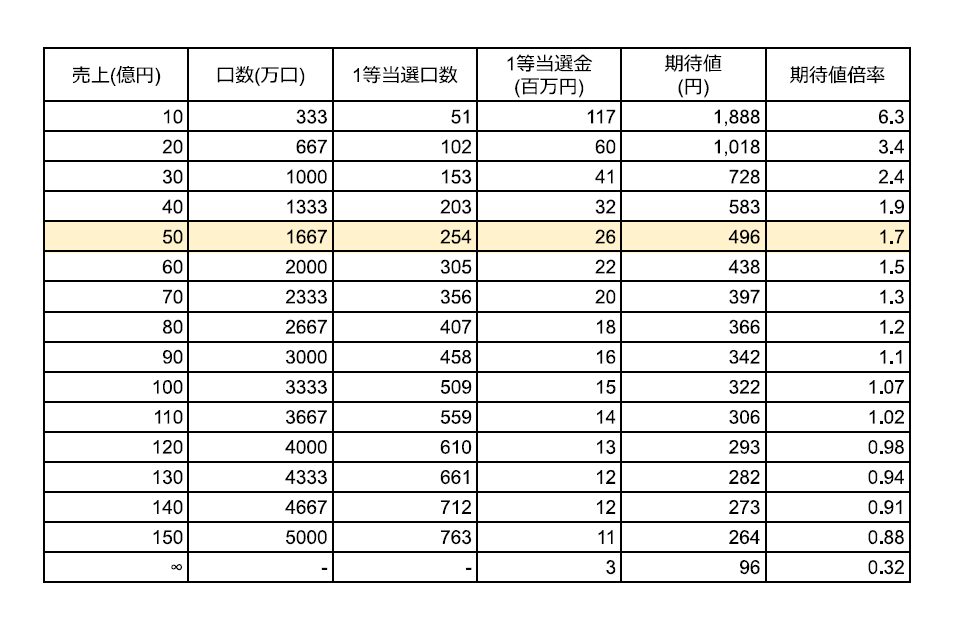
加えてキャリーオーバーがあったとしても参加者(=売上)が増えると、1等の当選者も増え、キャリーオーバー(今回でいうと58億円)の一人当たりの分配額は減少します。計算してみると、期待値が1.0を割り込んでしまうのは概ね100億円であることがわかります。今回の件がより多くの人に知れ渡ってしまうと、今後台風で同じ事象が起きたとしても、多くの参加者が現れることが想定され、参加者数(=売り上げ数)を意識しながらMEGABIGに参加しなければいけません。(もちろんキャリーオーバーの金額も。)
さらに仮に同じ事象が生じた場合に「いくら投資すれば良かったのか」を考えたいと思います。
大前提として、お金を賭ければ賭けるほど、1等が「6.5万分の1」と言えど大数の法則が効いてくるので、負ける確率が低下します。とはいえ一般人が数億円をすぐに用意できるわけではないので、一般人の心理状況(リスク許容度)として最低いくら賭ければ、「博打」ではなく「投資」になるのか考えてみました。
結論としては1億円
でした。自分の場合。もちろん実際には用意できないですが。理論上です。
考え方としては以下の観点で、一般的な投資対象(株式うや債券)と比べてリスクの観点でどうかということを比較してみました。無論、リターンの観点では期待値が1.7と圧倒的にプラスです。
- 株式投資と比較してマイナスリターンになる確率の比較
- 債券投資と比較してデフォルトになる確率の比較
株式は個別株を考えると個別性が高すぎて統計的な比較が難しいので、インデックス投資を想定しました。TOPIXやMSCI-KOKUSAIのインデックスであれば、概ね年間で期待リターン7%(期待値1.07)、リスクが15%と言われています。これを仮定して、マイナスリターン(1年後に0%以下になる確率)を計算してみると約32%になりました。
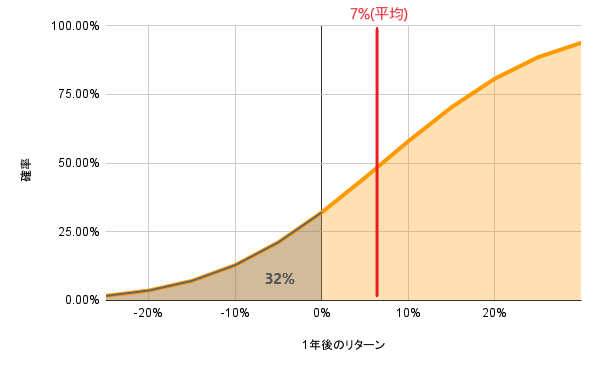
株式インデックス投資はほぼ全銘柄に投資しているのでマイナス50%はあれど全損(マイナス100%)は存在しません。一方で、MEGABIGは「1本も1等が当たらない」という可能性があり(とはいえ2等以下で投資額の30%は確実に返ってくる)、構造としては債券に近いように思いました。
債券もインデックス投資が存在するのでこれも全損はあり得ませんが、株式と異なって「格付け」という概念が存在するので、「格付け」ベースでのリスクでMEGABIGと比較してみることにしました。そうすると、「投資適格」と言われるカテゴリーの最低水準であるBBB格の全損確率は平均1%とのことです。
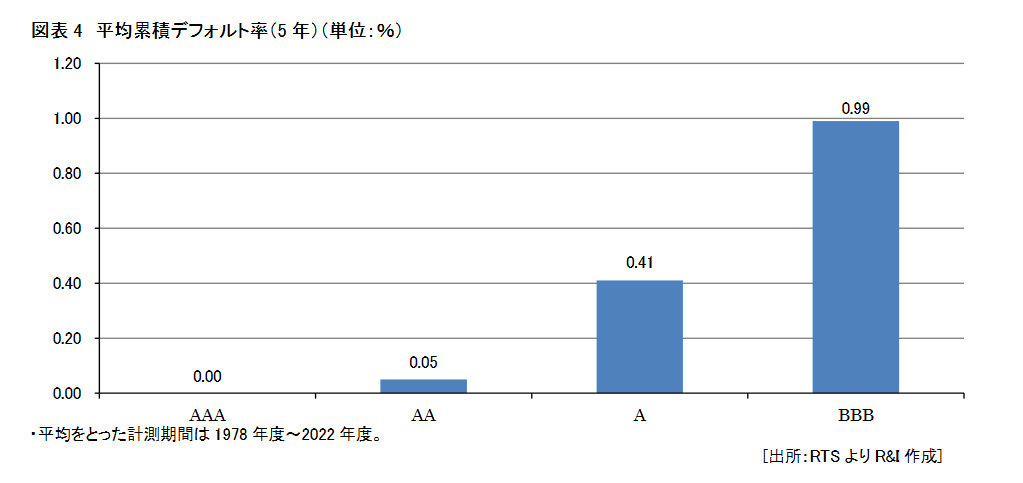
人間の心理的にも、全損する確率が10%と聞くと”あり得そう”と感じますが、数%と聞くと”滅多にないこと”だなと感じそうだなと思いました。(完全な主観)
ここまでの議論を振り返ると、「博打」から「投資」になるためには
- マイナスリターンになる確率が30%以下(勝つ確率が70%以上)
- 最悪のリスク(全損)となる確率は4%以下(四捨五入して0%)
という条件で探してみると前述の1億円が候補に上がりました。そういう意味では7500万円もこの条件に合う数字で、ご本人が意図してこの金額を集めたのか、偶然集まった金額がこれだったのかは分かりません。この計算では織り込んでいませんが、投資すればするほど負ける確率・全損確率は大数の法則によって下がりますが、通常6億円程度の売り上げを一人で引き上げることにもなるので、数億円以上の投資は逆に自分のリスクを上げてしまう恐れがあることには留意です。
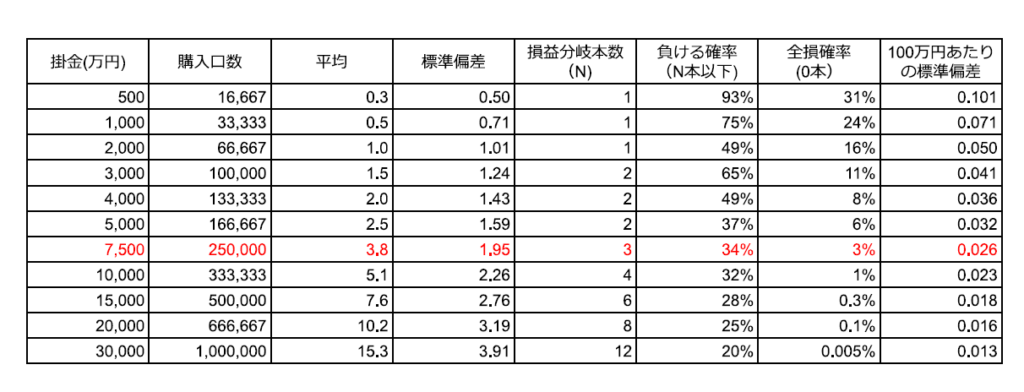
※1等は25百万円計算(自分が購入数を増やすことで当選金額が薄まることは考慮していない)
しかし、毎週コツコツとキャリーオーバーの分配を夢見て数口づつ買っていた人たちからすれば、普通の宝くじも買ったことないような人たちが圧倒的な資本を使って「夢」をかっさらっていってしまった今回の事象は少し寂しいような気がしました。自分はこういう人間なので宝くじを買ったことはありませんが、何を隠そう親は毎年10万円は「夢」見て宝くじを買っている側の人々なので。




